Olá galera! Acabei de me inscrever aqui e necessito de ajuda para resolver algumas funções de primeiro grau. Receio que não tenha visto esse tema com a devida profundidade pois não faço ideia nem por onde começar. O exercício diz o seguinte:
É dado que f(x) > 0, para todo x real, f(1) = 3 e f(u + v) = f(u) . f(v), para quaisquer números reais u e v. Calcule:
a.) f(2)
b.) f(0)
c.) f(1/2)
Eu tentei montar algum tipo de sistema para achar valores de u e v, mas percebi que não é por ai que devo começar, pois fazendo
u + v = 1
u . v = 3
onde, v = 1 - u
e substituindo u . (1 - u) = 3
simplificando e resolvendo, eu chego na equação de segundo grau - u² + u - 3, onde o delta é negativo, não possuindo raízes reais.
Não faço ideia do que fazer, por favor, me ajudem =(


 ;assim
;assim  .
.  ,concluímos que
,concluímos que  . Qual a resposta ?
. Qual a resposta ? 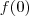 ? Podemos tomar
? Podemos tomar  e
e  ;assim ,
;assim ,  ,logo
,logo  e qual seria a resposta ?
e qual seria a resposta ?  ,como ficaria ??
,como ficaria ??

 , onde
, onde  é uma constante real, temos então
é uma constante real, temos então

 e então podemos determinar a função
e então podemos determinar a função 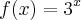 .
. e voce terá os valores das funções.
e voce terá os valores das funções. e
e 


 seria, transformando em raiz ficaria
seria, transformando em raiz ficaria ![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png) , correto?
, correto?
 .
.



