 por Larissa Valim » Dom Fev 24, 2013 16:12
por Larissa Valim » Dom Fev 24, 2013 16:12
(UFMG) A função
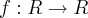
associa a cada número real x o menor inteiro maior do que 2x.
O valor de
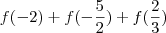
é:
a) -4
b) -3
c) -2
d) -1
d) 0
Minhas tentativas:Analisando f(-2):
(-2).2=-4
O menor inteiro maior que -4 é
-3.Analisando
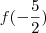
:
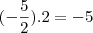
O menor inteiro maior que -5 é
-4.
Analisando
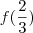
:
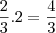
O menor inteiro maior que

é
2.
Logo, -3+(-4)+2=-5
Porém, não há essa resposta dentre as opções.
-
Larissa Valim
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Fev 24, 2013 15:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Dom Fev 24, 2013 17:06
por Cleyson007 » Dom Fev 24, 2013 17:06
Boa tarde Larissa!
Seja bem-vinda ao AjudaMatemática

Encontrei uma resolução na internet apesar de também não bater com o gabarito. Lá vai:
http://br.answers.yahoo.com/question/in ... 143AAUxthKVamos ver o que os nosso amigos dizem

Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Russman » Dom Fev 24, 2013 19:23
por Russman » Dom Fev 24, 2013 19:23
Eu concordo com o -5. A função associa números reais à inteiros, logo não há problema em termos 2x = 4/3.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Funções] Questão da UFMG
por SCHOOLGIRL+T » Qua Nov 07, 2012 20:53
- 2 Respostas
- 8133 Exibições
- Última mensagem por SCHOOLGIRL+T

Qui Nov 08, 2012 20:17
Funções
-
- Questão UFMG
por Guilherme Carvalho » Qui Mar 03, 2011 13:03
- 1 Respostas
- 4698 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 13:27
Álgebra Elementar
-
- Questão da UFMG
por Kelvin Brayan » Sáb Mar 12, 2011 17:19
- 1 Respostas
- 4941 Exibições
- Última mensagem por Rogerio Murcila

Qua Mar 16, 2011 23:42
Matemática Financeira
-
- Questão da UFMG
por Kelvin Brayan » Dom Mar 13, 2011 16:26
- 4 Respostas
- 2517 Exibições
- Última mensagem por Kelvin Brayan

Seg Mar 14, 2011 00:34
Cálculo: Limites, Derivadas e Integrais
-
- Questão UFMG
por Guilherme Carvalho » Qua Mar 16, 2011 16:39
- 5 Respostas
- 2907 Exibições
- Última mensagem por Kelvin Brayan

Ter Mar 22, 2011 00:23
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
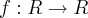 associa a cada número real x o menor inteiro maior do que 2x.
associa a cada número real x o menor inteiro maior do que 2x.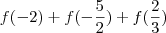 é:
é: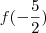 :
: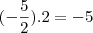
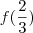 :
: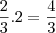
 é 2.
é 2.





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.