Considerando
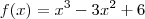
Temos

é estritamente crescente em
![I_1 = ]-\infty ,0] I_1 = ]-\infty ,0]](/latexrender/pictures/d8ce6acc624a27ef7489e70f5d73ef8c.png)
e
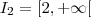
e decrescente
![I_ 3 = [0,2] I_ 3 = [0,2]](/latexrender/pictures/6404bf1ec78b8dcfd6431df56759dd09.png)
.
Vamos verificar em cada intervalo
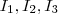
se há pelo menos um

em algum deles tal que

.
(1)
Como

, o termo dominante, possui grau impar ,
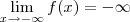
e
como
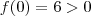
Assim ,existem
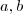
tais que
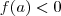
e
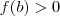
.Como

é contínua (Porque ? ) ,pelo TVI existe
![c \in [a,b] \subset I_1 c \in [a,b] \subset I_1](/latexrender/pictures/39388d28b38e710f4837403df0a7620a.png)
tal que
![f(c) = 0 \in [f(a),f(b)] f(c) = 0 \in [f(a),f(b)]](/latexrender/pictures/bf5bc82f80c34ebc04ba55cc717d6e57.png)
.
(2)
Como
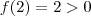
e
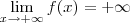
(Porque ?),concluímos que pelo TVI não existe

em

tal que

.
(3)
Segue de imediato de (1) e (2) que
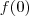
e
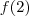
são ambos postivos ,sendo assim,
![0\notin [f(2),f(0)] 0\notin [f(2),f(0)]](/latexrender/pictures/e5d696bb5b221fdcd8d083947e8fa716.png)
, ou seja , não existe

em
![[0,
2] [0,
2]](/latexrender/pictures/5972b6c9e097c358fbe29f611f3dfd56.png)
tal que

.
Conclusão :

admite uma única raiz real ,pois, como já mencionado acima

é estritamente crescente em
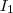
.

Para determinarmos o intervalo de amplitude 1 que contenha

,
veja que
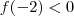
e
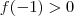
;assim
![\exists c \in [-2,-1] : f(c) = 0 \exists c \in [-2,-1] : f(c) = 0](/latexrender/pictures/1d757c5f4778d0217d58b052ec8df660.png)
.
Espero que ajude .
Editado erro de digitação .


 através de
através de 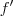 ?
? em
em ![[-2,-1] [-2,-1]](/latexrender/pictures/9b03926afdfad73896be89ba37623f7d.png) tal que
tal que ![f(c) = 0 \in [f(2),f(-1)]\subset D_f =\mathbb{R} f(c) = 0 \in [f(2),f(-1)]\subset D_f =\mathbb{R}](/latexrender/pictures/20e5665db757f8cbf7aa9790a0b08356.png) (OBS.: f é contínua )
(OBS.: f é contínua )
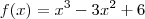
![I_1 = ]-\infty ,0] I_1 = ]-\infty ,0]](/latexrender/pictures/d8ce6acc624a27ef7489e70f5d73ef8c.png) e
e 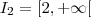 e decrescente
e decrescente ![I_ 3 = [0,2] I_ 3 = [0,2]](/latexrender/pictures/6404bf1ec78b8dcfd6431df56759dd09.png) .
.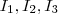 se há pelo menos um
se há pelo menos um  .
. , o termo dominante, possui grau impar ,
, o termo dominante, possui grau impar , 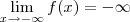
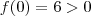
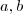 tais que
tais que 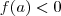 e
e 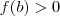 .Como
.Como ![c \in [a,b] \subset I_1 c \in [a,b] \subset I_1](/latexrender/pictures/39388d28b38e710f4837403df0a7620a.png) tal que
tal que ![f(c) = 0 \in [f(a),f(b)] f(c) = 0 \in [f(a),f(b)]](/latexrender/pictures/bf5bc82f80c34ebc04ba55cc717d6e57.png) .
. 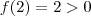 e
e 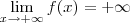 (Porque ?),concluímos que pelo TVI não existe
(Porque ?),concluímos que pelo TVI não existe  tal que
tal que 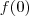 e
e 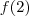 são ambos postivos ,sendo assim,
são ambos postivos ,sendo assim, ![0\notin [f(2),f(0)] 0\notin [f(2),f(0)]](/latexrender/pictures/e5d696bb5b221fdcd8d083947e8fa716.png) , ou seja , não existe
, ou seja , não existe ![[0,
2] [0,
2]](/latexrender/pictures/5972b6c9e097c358fbe29f611f3dfd56.png) tal que
tal que 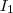 .
.
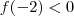 e
e 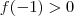 ;assim
;assim ![\exists c \in [-2,-1] : f(c) = 0 \exists c \in [-2,-1] : f(c) = 0](/latexrender/pictures/1d757c5f4778d0217d58b052ec8df660.png) .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)