 por timoteo » Dom Jan 20, 2013 19:55
por timoteo » Dom Jan 20, 2013 19:55
ola, estou tentando encontrar o dominio da funçao f(x)= 2 arc cos (x/2 + 3).
quando calculo eu faço assim...
cos f(x) = 2 . (x/2 + 3) -->
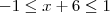
-->
S=[-7, -5].
porem a resposta do livro é realizada como se o dois nao multiplicasse com (cos f(x) = 2 . (x/2 + 3)).
ficando assim:
cosf(x) = x/2 + 3 -->
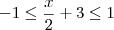
-->
S= [-8, -4].
parece-me que quando procura-se o dominio o dois nao tem relevancia. nao influencia no resultado final.
mas, verifique que o mesmo nao ocorre com a imagem; donde o dois ou qualquer n tem importancia no resultado final...
alguem poderia dizer se estou certo e o porque da aparente exclusão do dois no caso do dominio?
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por timoteo » Dom Jan 20, 2013 20:23
por timoteo » Dom Jan 20, 2013 20:23
compreende o valor dois ou n varia simplesmente o valor da imagem, pois se encontra na parte referente a imagem...

-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por e8group » Dom Jan 20, 2013 20:24
por e8group » Dom Jan 20, 2013 20:24
Boa noite .
Podemos escrever

como composição de duas outras funções multiplicada por uma função constante .
Sejam
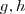
e

funções definidas por
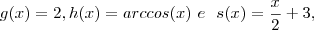
temos que ,
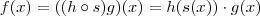
.
O domínio da função

será :
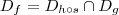
.
Como

e
![D_{h\circ s} = D_h \cap Im_s = [-1,1] D_{h\circ s} = D_h \cap Im_s = [-1,1]](/latexrender/pictures/3d9a9e6b7270822bd6c9561b1a375578.png)
.Desta forma ,
![D_f = D_{h\circ s} \cap D_g = [-1,1] D_f = D_{h\circ s} \cap D_g = [-1,1]](/latexrender/pictures/27053f5550c66bcc19c2c651d9496b49.png)
.
Como

é cosntante, segue que :
![s(x) \in [-1,1] s(x) \in [-1,1]](/latexrender/pictures/3fe2cf7194bc140437c37079dd518b15.png)
.
Ou seja ,
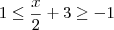
. Espero que ajude !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Seno e Coseno]help me?
por Giudav » Qui Mai 24, 2012 21:57
- 1 Respostas
- 3228 Exibições
- Última mensagem por Max Cohen

Sex Mai 25, 2012 01:38
Trigonometria
-
- inequações com seno e coseno
por ezidia51 » Qua Abr 04, 2018 17:57
- 3 Respostas
- 3937 Exibições
- Última mensagem por ezidia51

Qui Abr 05, 2018 13:09
Inequações
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3254 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2890 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- [Dominio] Cálculo 2- Domínio
por Saturnino Nataniel » Seg Fev 25, 2013 14:09
- 2 Respostas
- 1724 Exibições
- Última mensagem por timoteo

Ter Abr 09, 2013 12:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
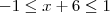 -->
-->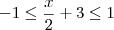 -->
-->

 como composição de duas outras funções multiplicada por uma função constante .
como composição de duas outras funções multiplicada por uma função constante .  e
e  funções definidas por
funções definidas por 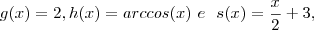
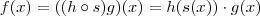 .
. 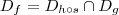 .
.  e
e ![D_{h\circ s} = D_h \cap Im_s = [-1,1] D_{h\circ s} = D_h \cap Im_s = [-1,1]](/latexrender/pictures/3d9a9e6b7270822bd6c9561b1a375578.png) .Desta forma ,
.Desta forma , ![D_f = D_{h\circ s} \cap D_g = [-1,1] D_f = D_{h\circ s} \cap D_g = [-1,1]](/latexrender/pictures/27053f5550c66bcc19c2c651d9496b49.png) .
. é cosntante, segue que :
é cosntante, segue que : ![s(x) \in [-1,1] s(x) \in [-1,1]](/latexrender/pictures/3fe2cf7194bc140437c37079dd518b15.png) .
. 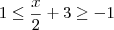 . Espero que ajude !
. Espero que ajude !
 .
.



