 por MathNewbie » Seg Out 08, 2012 14:33
por MathNewbie » Seg Out 08, 2012 14:33
Bom dia, estou resolvendo uma questão de álgebra linear 2 e epanquei no meio do caminho.
A questão é a seguinte:
Determinar a matriz P tal que:
![[T]\gamma=P{^{-1}}\cdot [T]\beta\cdot P [T]\gamma=P{^{-1}}\cdot [T]\beta\cdot P](/latexrender/pictures/62dcfcb8b45555e2f4e19885bee6e381.png)
, sabendo que:

;

e

.
Eu comecei a resolver e achei assim:
Para

:


Logo:
![[T]\beta =\begin{bmatrix} 1&-1 \\ 1&1 \end{bmatrix} [T]\beta =\begin{bmatrix} 1&-1 \\ 1&1 \end{bmatrix}](/latexrender/pictures/e0eec0ece8d206dc864eedb6a349b70a.png)
Agora para


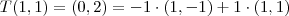
Logo:
![[T]\gamma =\begin{bmatrix} 1 & -1\\ 1 & 1 \end{bmatrix} [T]\gamma =\begin{bmatrix} 1 & -1\\ 1 & 1 \end{bmatrix}](/latexrender/pictures/40aaefec2c7ddf881e12b29a6c64c111.png)
Foi ai aonde eu empaquei, eu estou achando que:
![P^{-1}=[T]_{\beta }^{\gamma } P^{-1}=[T]_{\beta }^{\gamma }](/latexrender/pictures/239e79927402b50d448083e2eadc8d8c.png)
Estou certo ?
Me ajudem a resolver este problema, que aparentemente me pareceu simples mas não estou conseguindo!
-
MathNewbie
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 08, 2012 14:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Ter Out 09, 2012 10:19
por young_jedi » Ter Out 09, 2012 10:19
voce pode dizer que se
![[T]_{\gamma}=P^{-1}.[T]_{\beta}.P [T]_{\gamma}=P^{-1}.[T]_{\beta}.P](/latexrender/pictures/d79a02a7124ddc032f149efe08f62e57.png)
então
![P.[T]_{\gamma}=P.P^{-1}.[T]_{\beta}.P P.[T]_{\gamma}=P.P^{-1}.[T]_{\beta}.P](/latexrender/pictures/8a730c6d320724ff5b4a33073882e116.png)
mais

então
![P.[T]_{\gamma}=[T]_{\beta}.P P.[T]_{\gamma}=[T]_{\beta}.P](/latexrender/pictures/9b3b6e1438104b32e0a4015629b96787.png)
tente determinar P apartir disto
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MathNewbie » Ter Out 09, 2012 13:19
por MathNewbie » Ter Out 09, 2012 13:19
young_jedi escreveu:voce pode dizer que se
![[T]_{\gamma}=P^{-1}.[T]_{\beta}.P [T]_{\gamma}=P^{-1}.[T]_{\beta}.P](/latexrender/pictures/d79a02a7124ddc032f149efe08f62e57.png)
então
![P.[T]_{\gamma}=P.P^{-1}.[T]_{\beta}.P P.[T]_{\gamma}=P.P^{-1}.[T]_{\beta}.P](/latexrender/pictures/8a730c6d320724ff5b4a33073882e116.png)
mais

então
![P.[T]_{\gamma}=[T]_{\beta}.P P.[T]_{\gamma}=[T]_{\beta}.P](/latexrender/pictures/9b3b6e1438104b32e0a4015629b96787.png)
tente determinar P apartir disto
Obrigado, por esse método fica mais fácil acharmos P.
No final acredito que P seja a matriz da transformada, pois
![[T]_{\gamma} [T]_{\gamma}](/latexrender/pictures/c3ff5cd975736bd32d2683f7c0e25e55.png)
e
![[T]_{\beta} [T]_{\beta}](/latexrender/pictures/f2f8898940de3f214f7a23c87a4c7b36.png)
são iguais. Ainda não resolvi pois estou ocupado no momento mas acredito que seja a saída mais fácil.
Vlw!
-
MathNewbie
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 08, 2012 14:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matriz transformada em sistema
por Claudin » Qui Fev 16, 2012 18:17
- 4 Respostas
- 2020 Exibições
- Última mensagem por Claudin

Qui Fev 16, 2012 20:20
Matrizes e Determinantes
-
- Duvida para achar uma Matriz X
por njaneto » Qua Mar 18, 2015 12:43
- 3 Respostas
- 6037 Exibições
- Última mensagem por Cleyson007

Qua Mar 18, 2015 22:55
Matrizes e Determinantes
-
- Nao consigo achar a forma reduzida da matriz..
por PeIdInHu » Seg Jun 14, 2010 23:07
- 1 Respostas
- 2580 Exibições
- Última mensagem por PeIdInHu

Seg Jun 14, 2010 23:55
Matrizes e Determinantes
-
- [TRANSFORMADA DE LAPLACE]
 por liviabgomes » Qui Dez 01, 2011 15:19
por liviabgomes » Qui Dez 01, 2011 15:19
- 1 Respostas
- 1221 Exibições
- Última mensagem por LuizAquino

Seg Dez 05, 2011 10:19
Cálculo: Limites, Derivadas e Integrais
-
- Transformada de Laplace
por Russman » Sex Mai 04, 2012 01:13
- 2 Respostas
- 1580 Exibições
- Última mensagem por pvgomes07

Sex Ago 10, 2012 13:11
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![[T]\gamma=P{^{-1}}\cdot [T]\beta\cdot P [T]\gamma=P{^{-1}}\cdot [T]\beta\cdot P](/latexrender/pictures/62dcfcb8b45555e2f4e19885bee6e381.png) , sabendo que:
, sabendo que:  ;
;  e
e  .
. :
:

![[T]\beta =\begin{bmatrix} 1&-1 \\ 1&1 \end{bmatrix} [T]\beta =\begin{bmatrix} 1&-1 \\ 1&1 \end{bmatrix}](/latexrender/pictures/e0eec0ece8d206dc864eedb6a349b70a.png)


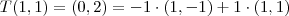
![[T]\gamma =\begin{bmatrix} 1 & -1\\ 1 & 1 \end{bmatrix} [T]\gamma =\begin{bmatrix} 1 & -1\\ 1 & 1 \end{bmatrix}](/latexrender/pictures/40aaefec2c7ddf881e12b29a6c64c111.png)
![P^{-1}=[T]_{\beta }^{\gamma } P^{-1}=[T]_{\beta }^{\gamma }](/latexrender/pictures/239e79927402b50d448083e2eadc8d8c.png)


![[T]_{\gamma}=P^{-1}.[T]_{\beta}.P [T]_{\gamma}=P^{-1}.[T]_{\beta}.P](/latexrender/pictures/d79a02a7124ddc032f149efe08f62e57.png)
![P.[T]_{\gamma}=P.P^{-1}.[T]_{\beta}.P P.[T]_{\gamma}=P.P^{-1}.[T]_{\beta}.P](/latexrender/pictures/8a730c6d320724ff5b4a33073882e116.png)

![P.[T]_{\gamma}=[T]_{\beta}.P P.[T]_{\gamma}=[T]_{\beta}.P](/latexrender/pictures/9b3b6e1438104b32e0a4015629b96787.png)

![[T]_{\gamma} [T]_{\gamma}](/latexrender/pictures/c3ff5cd975736bd32d2683f7c0e25e55.png) e
e ![[T]_{\beta} [T]_{\beta}](/latexrender/pictures/f2f8898940de3f214f7a23c87a4c7b36.png) são iguais. Ainda não resolvi pois estou ocupado no momento mas acredito que seja a saída mais fácil.
são iguais. Ainda não resolvi pois estou ocupado no momento mas acredito que seja a saída mais fácil. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
