 por mih123 » Ter Ago 28, 2012 15:40
por mih123 » Ter Ago 28, 2012 15:40
Boa tarde! Estou com dúvida em quando vai existir limite ou não limite. Quando os limites laterais são diferentes não tem limite.
Dessa forma, para saber se vai existir o limite eu vou ter que fazer duas vezes???
Nesse caso aqui:
![\lim_{x\to-3}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}} \lim_{x\to-3}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}}](/latexrender/pictures/571499d787ccf098f483cc30395a21fa.png)
No Wolfram, mostra que não existe.Então,sempre vou ter que fazer de dois jeitos??
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Ter Ago 28, 2012 16:19
por MarceloFantini » Ter Ago 28, 2012 16:19
Sim, só que você terá que calcular com a variável tendendo pela direita e depois pela esquerda. Em notação,
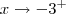
e

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Ter Ago 28, 2012 16:21
por Claudin » Ter Ago 28, 2012 16:21
mih123 escreveu:Boa tarde! Estou com dúvida em quando vai existir limite ou não limite. Quando os limites laterais são diferentes não tem limite.
Dessa forma, para saber se vai existir o limite eu vou ter que fazer duas vezes???
Sim.
mih123 escreveu:Nesse caso aqui:
![\lim_{x\to-3}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}} \lim_{x\to-3}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}}](/latexrender/pictures/571499d787ccf098f483cc30395a21fa.png)
No Wolfram, mostra que não existe.Então,sempre vou ter que fazer de dois jeitos??
Nesse caso você terá de resolver os seguintes limites:
![\lim_{x\to-3^{-}}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}} \lim_{x\to-3^{-}}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}}](/latexrender/pictures/994646282561bfb86658a6dbacb8c06f.png)
e
![\lim_{x\to-3^{+}}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}} \lim_{x\to-3^{+}}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}}](/latexrender/pictures/3b0d07a4a0e7d8736363cef0c62ae480.png)
Caso o resultado for igual, é sinal que o limite existe, caso o resultado for diferente, você prova que não existe limite.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Ago 29, 2012 07:50
por LuizAquino » Qua Ago 29, 2012 07:50
mih123 escreveu:Boa tarde! Estou com dúvida em quando vai existir limite ou não limite. Quando os limites laterais são diferentes não tem limite.
Dessa forma, para saber se vai existir o limite eu vou ter que fazer duas vezes???
Se você desejar assistir uma videoaula sobre Limites Laterais, eu gostaria de recomendar a videoaula "03. Cálculo I - Limites Laterais". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por mih123 » Qua Ago 29, 2012 15:55
por mih123 » Qua Ago 29, 2012 15:55
Olá gente, LuizAquino eu assisti sua aula. Eu continuo com dúvidas,porque todos os exercícios de vários livros que eu olhei nos limites laterais, há duas funções uma para os menores outra para os maiores. E no caso aqui só tem uma função.
Desculpa gente, exemplo de limite que eu coloquei anteriormente existe sim.É porque na hora de colocar aqui eu me confundi.O que não existe é esse aqui:
![\lim_{x\to3}\frac{{x}^{2}+\sqrt[3]{x-3}-9}{\sqrt[3]{9-x\sqrt[2]{4x-3}}} \lim_{x\to3}\frac{{x}^{2}+\sqrt[3]{x-3}-9}{\sqrt[3]{9-x\sqrt[2]{4x-3}}}](/latexrender/pictures/e78dbfc2bdcb125b7026c207e7f66e01.png)
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Claudin » Qua Ago 29, 2012 16:21
por Claudin » Qua Ago 29, 2012 16:21
mih123 escreveu:Olá gente, LuizAquino eu assisti sua aula. Eu continuo com dúvidas,porque todos os exercícios de vários livros que eu olhei nos limites laterais, há duas funções uma para os menores outra para os maiores. E no caso aqui só tem uma função.
Sim, deixe em qual ponto é realmente a sua dúvida, seja na resolução ou no entendimento do conceito de limites laterais, tendo em vista que as aulas não foram uma boa ajuda para sanar sua dúvida, se precisar de alguma resolução ou algo similar, poste aqui.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mih123 » Qua Ago 29, 2012 16:27
por mih123 » Qua Ago 29, 2012 16:27
O conceito eu entendi. O problema é que eu tenho uma lista de exercícios pra fazer.Daí, me aparece exercícios que os limites não existem.
Então, eu não sei o que fazer pra descobrir se existe ou não.
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Claudin » Qua Ago 29, 2012 16:55
por Claudin » Qua Ago 29, 2012 16:55
Basta fazê-los pela esquerda e pela direita, se der igual o limite existe, se for diferente o limite não existe, basicamente é isso.
Se quiser postar exercícios que você tem dúvida pode postar também.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Ago 29, 2012 16:59
por MarceloFantini » Qua Ago 29, 2012 16:59
Se for postar, por favor poste em novos tópicos, para manter a organização do fórum.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Limites laterais
por TonyR » Sáb Set 01, 2012 13:18
- 1 Respostas
- 1547 Exibições
- Última mensagem por LuizAquino

Sáb Set 01, 2012 15:41
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2796 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES LATERAIS
por Fabio Cabral » Qua Out 06, 2010 11:48
- 6 Respostas
- 4248 Exibições
- Última mensagem por Fabio Cabral

Qui Out 07, 2010 11:04
Funções
-
- Limites laterais
por valeuleo » Sáb Abr 09, 2011 21:07
- 8 Respostas
- 5900 Exibições
- Última mensagem por MarceloFantini

Dom Abr 10, 2011 21:00
Cálculo: Limites, Derivadas e Integrais
-
- Limites Laterais
por FernandaBS » Sex Mai 25, 2012 18:04
- 3 Respostas
- 3713 Exibições
- Última mensagem por Guill

Sáb Mai 26, 2012 15:26
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\to-3}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}} \lim_{x\to-3}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}}](/latexrender/pictures/571499d787ccf098f483cc30395a21fa.png)

![\lim_{x\to-3}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}} \lim_{x\to-3}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}}](/latexrender/pictures/571499d787ccf098f483cc30395a21fa.png)

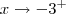 e
e  .
.

![\lim_{x\to-3^{-}}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}} \lim_{x\to-3^{-}}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}}](/latexrender/pictures/994646282561bfb86658a6dbacb8c06f.png)
![\lim_{x\to-3^{+}}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}} \lim_{x\to-3^{+}}\frac{\sqrt[2]{\sqrt[3]{-9x}+1}-2}{2-\sqrt[3]{x+11}}](/latexrender/pictures/3b0d07a4a0e7d8736363cef0c62ae480.png)


![\lim_{x\to3}\frac{{x}^{2}+\sqrt[3]{x-3}-9}{\sqrt[3]{9-x\sqrt[2]{4x-3}}} \lim_{x\to3}\frac{{x}^{2}+\sqrt[3]{x-3}-9}{\sqrt[3]{9-x\sqrt[2]{4x-3}}}](/latexrender/pictures/e78dbfc2bdcb125b7026c207e7f66e01.png)






 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.