![f(x)=\sqrt[]{} 3-\left|x-2 \right|/x f(x)=\sqrt[]{} 3-\left|x-2 \right|/x](/latexrender/pictures/9403aaec0fed90ec5c2d1b0d89abc6c9.png) .
.a) Dê o domínio da função f. responda na forma de intervalo ou união de intervalos, conforme seja o caso.
b) Verifique se 2 pertence Im(f), ou seja, verifique se existe x E Dom(f), tal que f(x)=2.
Minha resolução até onde consegui é a seguinte, só não sei se estou seguindo um raciocínio certo
x tem que ser diferente de 0
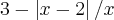 >= 0
>= 0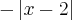 >= -3 (x-1)
>= -3 (x-1) <=3
<=3-3<= x<= 3


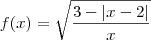


 .
.
 :
: