 por leticy » Sáb Ago 11, 2012 20:46
por leticy » Sáb Ago 11, 2012 20:46
Pessoal, estou com uma dúvida, tentei resolver esse exercício varias vezes e não consigo chegar ao resultado.
Eu tenho a resposta, mas não chego. Segue.
Simplifique a expressão:
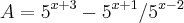
Eu fiz alguns cálculos, o que consigo chegar é:

Aqui não sei mais o que fazer, o que preciso fazer?
-
leticy
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Ago 11, 2012 20:33
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: administração
- Andamento: cursando
 por e8group » Sáb Ago 11, 2012 21:20
por e8group » Sáb Ago 11, 2012 21:20
Boa noite , sua expressão se resume a isto
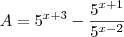
? Se a resposta for sim observe que ,
![A = 5^{x+3} -\frac{5^{x+1}}{5^{x-2}} = 5^{x+3} -5^{x+1 \ -\left[x-2\right]} = 5^{x+3} -5^{3} =5^3(5^x-1)=125(5^x-1). A = 5^{x+3} -\frac{5^{x+1}}{5^{x-2}} = 5^{x+3} -5^{x+1 \ -\left[x-2\right]} = 5^{x+3} -5^{3} =5^3(5^x-1)=125(5^x-1).](/latexrender/pictures/3e83c4883f6d79145396e376e4db553e.png)
Propriedades :
i)

ii)
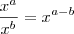
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sáb Ago 11, 2012 22:25
por MarceloFantini » Sáb Ago 11, 2012 22:25
Entretanto, se a expressão for
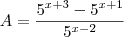
então tudo será diferente. Qual delas?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por leticy » Dom Ago 12, 2012 09:01
por leticy » Dom Ago 12, 2012 09:01
Olá MarceloFantini, primeiramente, agradeço por sua atenção.
A expressão da pergunta é a segunda, aonde:
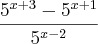
Me perdoe pelo equivoco, sou novata aqui.
-
leticy
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Ago 11, 2012 20:33
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: administração
- Andamento: cursando
 por MarceloFantini » Dom Ago 12, 2012 09:38
por MarceloFantini » Dom Ago 12, 2012 09:38
Sem problemas. Note que
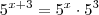
,

e
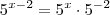
. Daí,
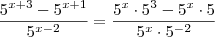
.
Ponha
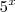
em evidência e está tudo resolvido.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por leticy » Dom Ago 12, 2012 10:27
por leticy » Dom Ago 12, 2012 10:27
MarceloFantini, foi exatamente ai que parei, até ai eu fui normalmente pelas propriedades da potenciação, agora não entendi como colocar o
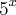
em evidência. Posso fazer isso baseado em que? como posso fazer essa operação de colocar uma letra em evidência? Muito obrigada de novo pela sua atenção.
-
leticy
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Ago 11, 2012 20:33
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: administração
- Andamento: cursando
 por MarceloFantini » Dom Ago 12, 2012 11:16
por MarceloFantini » Dom Ago 12, 2012 11:16
Não é uma letra, é um número. Temos uma função real
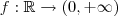
,
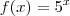
, que leva números reais em números positivos maiores que zero. Além disso, lembre-se que valem todas as regras algébricas usuais: distributiva, troca de ordem na multiplicação e soma, etc. Pode parecer estranho porque o expoente é variável, mas ele se comporta exatamente como um número porque ele é um número.
Em todo caso,

Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [potenciação] raiz cúbica com potenciação
por JKS » Qua Mar 06, 2013 17:41
- 2 Respostas
- 2292 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:43
Álgebra Linear
-
- [potenciação] módulo com potenciação
por JKS » Qua Mar 06, 2013 17:54
- 2 Respostas
- 1739 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:53
Equações
-
- POTENCIAÇÃO
por DANIELA » Sex Set 25, 2009 16:48
- 5 Respostas
- 3746 Exibições
- Última mensagem por DanielFerreira

Seg Set 28, 2009 10:20
Álgebra Elementar
-
- potenciação
por leandrofelip » Ter Fev 23, 2010 00:10
- 1 Respostas
- 2025 Exibições
- Última mensagem por Marcampucio

Ter Fev 23, 2010 12:56
Sistemas de Equações
-
- POTENCIACAO
por CaAtr » Ter Mar 09, 2010 20:23
- 3 Respostas
- 2294 Exibições
- Última mensagem por CaAtr

Ter Mar 09, 2010 22:17
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
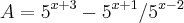


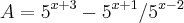


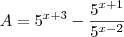 ? Se a resposta for sim observe que ,
? Se a resposta for sim observe que ,![A = 5^{x+3} -\frac{5^{x+1}}{5^{x-2}} = 5^{x+3} -5^{x+1 \ -\left[x-2\right]} = 5^{x+3} -5^{3} =5^3(5^x-1)=125(5^x-1). A = 5^{x+3} -\frac{5^{x+1}}{5^{x-2}} = 5^{x+3} -5^{x+1 \ -\left[x-2\right]} = 5^{x+3} -5^{3} =5^3(5^x-1)=125(5^x-1).](/latexrender/pictures/3e83c4883f6d79145396e376e4db553e.png)

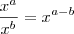 .
.
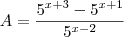


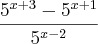

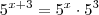 ,
,  e
e 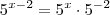 . Daí,
. Daí,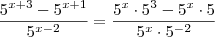 .
.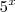 em evidência e está tudo resolvido.
em evidência e está tudo resolvido.

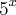 em evidência. Posso fazer isso baseado em que? como posso fazer essa operação de colocar uma letra em evidência? Muito obrigada de novo pela sua atenção.
em evidência. Posso fazer isso baseado em que? como posso fazer essa operação de colocar uma letra em evidência? Muito obrigada de novo pela sua atenção.
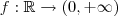 ,
, 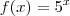 , que leva números reais em números positivos maiores que zero. Além disso, lembre-se que valem todas as regras algébricas usuais: distributiva, troca de ordem na multiplicação e soma, etc. Pode parecer estranho porque o expoente é variável, mas ele se comporta exatamente como um número porque ele é um número.
, que leva números reais em números positivos maiores que zero. Além disso, lembre-se que valem todas as regras algébricas usuais: distributiva, troca de ordem na multiplicação e soma, etc. Pode parecer estranho porque o expoente é variável, mas ele se comporta exatamente como um número porque ele é um número.

