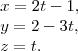por Claudin » Ter Jul 17, 2012 03:18
por Claudin » Ter Jul 17, 2012 03:18
Determine a equação paramétrica da reta
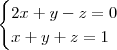
Não sei achar, pois não tenho nenhum ponto da reta
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Ter Jul 17, 2012 03:42
por MarceloFantini » Ter Jul 17, 2012 03:42
Somando as duas equações temos
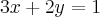
, daí
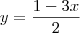
. Substituindo para z segue
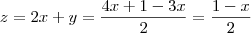
. Podemos adotar o parâmetro

e portanto
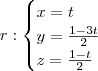
.
Sugiro que você estude os conteúdos com o livro escrito pelo Reginaldo Santos, está disponível para download. Você deveria saber que a interseção de dois planos em
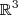
, quando não paralelos, é uma reta e assim resolver o sistema.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Ter Jul 17, 2012 15:56
por Claudin » Ter Jul 17, 2012 15:56
Na minha sala esse livro do Reginaldo Santos foi quase 90% que achou dificil de ser compreendido.
Na ocasião acima o z=x+1/2, o correto não seria assim?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Ter Jul 17, 2012 16:05
por Claudin » Ter Jul 17, 2012 16:05
No gabarito está diferente, pois adotou z=t
e substituindo a equação 1, quando acha o valor de y, quando substituir novamente para encontrar o valor de x, não consegue chegar a um resultado pois terá em uma equação duas incógnitas, sendo elas x e y.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Ter Jul 17, 2012 16:16
por MarceloFantini » Ter Jul 17, 2012 16:16
A outra recomendação é o livro de geometria analítica por Paulo Boulos. Mais tranquilo que estes dois será quase impossível.
A propósito, sim:
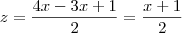
. Obrigado.
Não entendo o que quis dizer com "substituindo a equação 1" em diante. Para adotar o parâmetro

basta escrever

e

em função de z.
Subtraia a primeira da segunda, vem
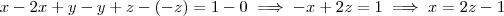
. Voltando na segunda temos
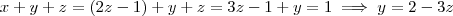
.
Adote

e portanto
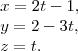
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Ter Jul 17, 2012 18:22
por Claudin » Ter Jul 17, 2012 18:22
Obrigado pela resposta.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações de plano] encontrar a equação de um plano
por GHT1810 » Ter Jul 03, 2018 19:42
- 0 Respostas
- 5269 Exibições
- Última mensagem por GHT1810

Ter Jul 03, 2018 19:42
Geometria Analítica
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14857 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
-
- [Equação do Plano Tangente - Plano Paralalelo]
por raimundoocjr » Qui Out 24, 2013 22:10
- 0 Respostas
- 2704 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- Plano
por Rhyu » Dom Abr 08, 2012 10:57
- 2 Respostas
- 1915 Exibições
- Última mensagem por MarceloFantini

Seg Abr 09, 2012 03:40
Geometria Analítica
-
- Plano
por Claudin » Sex Jul 06, 2012 12:32
- 2 Respostas
- 1748 Exibições
- Última mensagem por Claudin

Sex Jul 06, 2012 16:23
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
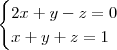

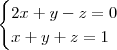

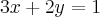 , daí
, daí 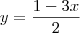 . Substituindo para z segue
. Substituindo para z segue 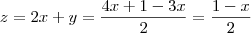 . Podemos adotar o parâmetro
. Podemos adotar o parâmetro  e portanto
e portanto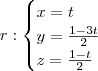 .
.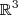 , quando não paralelos, é uma reta e assim resolver o sistema.
, quando não paralelos, é uma reta e assim resolver o sistema.



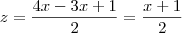 . Obrigado.
. Obrigado. basta escrever
basta escrever  e
e  em função de z.
em função de z.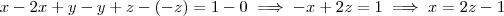 . Voltando na segunda temos
. Voltando na segunda temos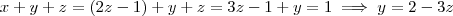 .
. e portanto
e portanto