 por citadp » Qui Jun 21, 2012 07:52
por citadp » Qui Jun 21, 2012 07:52
Tenho este exercicio:
Uma fábrica incorpora na sua produção um certo tipo de peças, que compra a três fornecedores( fornecedor I, fornecedor II, fornecedor III) nas seguintes proporções: 0.4 , 0.35 e 0.25. Da experiência passada, os responsáveis da fábrica sabem que 2% das peças oriundas do fornecedor I são defeituosas euq e essa percentagem é de 5% para o fornecedor II; sabem, ainda que 3.55% da totalidade de peças, deste tipo, que compram são defeituosas.
Calcule a percentagem de peças defeituosas fornecidas pelo fornecedor III.
Eu estava a fazer que
x----------3.55%
25%---------100%
(3.55 * 25)/100 = 0.88
Também já fiz que :
2----------100
x----------3.55
(2*3.55)/100= 0.071
5----------100
x----------3.55
(5*3.55)/100=0.1775
Depois fiz : 0.071+0.1775+ x = 3.55 <=> x= 3.30 a percentagem de defeito da III, gostaria que me dissessem se está bem ou mal, e que me ajudem sff!
Acho que está mal, não estou a conseguir achar essa percentagem de nenhuma maneira.
-
citadp
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Jun 02, 2012 13:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Informática
- Andamento: cursando
 por e8group » Qui Jun 21, 2012 11:29
por e8group » Qui Jun 21, 2012 11:29
Atribuindo uma variável x para peça .
Número total de peças =
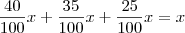
.
De forma análoga , Número total de peças defeituosas =
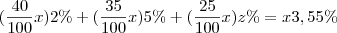
. Ou Seja , z = 4 % .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por citadp » Qui Jun 21, 2012 12:28
por citadp » Qui Jun 21, 2012 12:28
Muito obrigada.
Tenho outra dúvida que é a seguinte. X -> A, Y->B
X/Y 0 1 2
0 0.10 0.20 0.10
1 a 0.16 b
2 0.04 0.12 0.08
Determinar a e b sabendo que a loja vende em média 1.12 discos de marca B.
Ora o que eu estive a fazer foi:
0.10+0.20+0.10+a+0.16+b+0.04+0.12+0.08 = 1
a+ b =0.20
o valor designado em média, não consigo entender se é E(X), ou média mesmo.
-
citadp
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Jun 02, 2012 13:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Informática
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com Probabilidades
por BR51 » Qui Jun 03, 2010 21:33
- 0 Respostas
- 2301 Exibições
- Última mensagem por BR51

Qui Jun 03, 2010 21:33
Estatística
-
- [Probabilidades] ajuda
por XYZ » Sex Jan 13, 2012 13:27
- 3 Respostas
- 2391 Exibições
- Última mensagem por ant_dii

Sáb Jan 14, 2012 03:40
Estatística
-
- Estatística e probabilidades [ajuda]
por citadp » Sáb Jun 02, 2012 13:18
- 2 Respostas
- 4301 Exibições
- Última mensagem por nandabhz

Dom Jun 03, 2012 16:53
Probabilidade
-
- probabilidades cartas - Ajuda res.exercicio
por wilsonvicen7e » Qua Mar 20, 2013 23:12
- 2 Respostas
- 2135 Exibições
- Última mensagem por wilsonvicen7e

Qui Mar 21, 2013 14:47
Probabilidade
-
- Probabilidades - cálculo probabilidades e condicionada
por carlosmartins » Dom Set 21, 2014 18:58
- 0 Respostas
- 2959 Exibições
- Última mensagem por carlosmartins

Dom Set 21, 2014 18:58
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


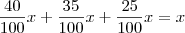 .
.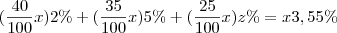 . Ou Seja , z = 4 % .
. Ou Seja , z = 4 % .