Empacado em mais um exercício...
O ponto P (3,3) é o centro de um feixe de retas no plano cartesiano . Determine as equações das retas desses feixe, perpendiculares entre si, que interceptam o eixo Ox nos pontos A e B, e tais que a distância entre eles seja 15/2.
Bom, primeiro eu pensei que se as duas retas fazem parte de um feixe de retas, então as duas retas vão concorrer no ponto P (3,3). Se elas são perpendiculares entre si, um dos angulos é 90º e os outros 2 são 45º (que são os angulos formados com o eixo x). Logo, penso que não seja necessário saber que a distancia seja 15/2 já que tenho o coeficiente angular de cada uma. Encontrei y+x =0 o que não condiz... a resposta. Queria saber qual foi o meu erro nesse raciocínio. Tentei de uma segunda maneira: Chamei o ponto A de (a,0), e o ponto B de (b,0). Utilizando a fórmula da distância para calcular a distância entre A e B e igualando a 15/2 eu encontrei uma relação tal que a = 15/2 +b. Aí eu fiz o determinante com os pontos A e o ponto P para encontrar a equação da reta relativa a ao ponto A. Encontrei a equação 6x + y(9+2b) - 45 -6b = 0. Penso que o coeficiente angular será 1 ou - 1 aí eu fiz -6/9+2b para as duas possibilidades, mas ainda assim não dá certo. Qual o meu erro? Grato desde já !


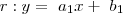 .
.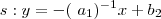 .
. 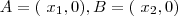 ,temos que :
,temos que :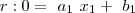
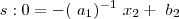 .
.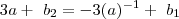 . Portanto ,
. Portanto , 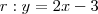
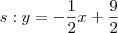

 .
.
 :
: