 por jhonniewalk » Qui Mai 24, 2012 16:49
por jhonniewalk » Qui Mai 24, 2012 16:49
Olá a todos,
Estou com algumas dúvidas em algumas derivadas, não tem haver com regras de derivação mas sim com simplificações com radicais e exponenciais.
Um dos exercícios é este:
![f(x)= \sqrt[]{\frac{3}{{x}^{5}}} f(x)= \sqrt[]{\frac{3}{{x}^{5}}}](/latexrender/pictures/6ece9ac4538bf0ea0bb303ed33d0a445.png)
A resolução do exercício é:
![f(x)=\frac{-5\sqrt[]{3}}{2\sqrt[]{{x}^{7}}} f(x)=\frac{-5\sqrt[]{3}}{2\sqrt[]{{x}^{7}}}](/latexrender/pictures/fa5b5f0eb3f6ee8718cb2ba5438439dd.png)
Os meus cálculos:
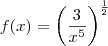
=
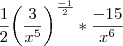
=
![\frac{1}{2\sqrt[]{}\frac{3}{{x}^{5}}}*\frac{-15}{{x}^{6}} \frac{1}{2\sqrt[]{}\frac{3}{{x}^{5}}}*\frac{-15}{{x}^{6}}](/latexrender/pictures/bffa052dc06a03638d03d8e1ec095f83.png)
=
![\frac{-15}{2 {x}^{6}\sqrt[]{}\frac{3}{{x}^{5}}} \frac{-15}{2 {x}^{6}\sqrt[]{}\frac{3}{{x}^{5}}}](/latexrender/pictures/57bf6c56f7959b40bc1afbebbe32f813.png)
Não sei simplificar mais do que isto

Onde posso ler sobre simplificações?
Obrigado
-
jhonniewalk
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mai 24, 2012 15:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecanica
- Andamento: cursando
 por DanielFerreira » Qui Mai 24, 2012 19:44
por DanielFerreira » Qui Mai 24, 2012 19:44
Jhonniewalk,
seja bem vindo!
Tente fazer o seguinte:
![f(x) = \sqrt[]{\frac{3}{x^5}} f(x) = \sqrt[]{\frac{3}{x^5}}](/latexrender/pictures/9736ee344761b5f3cbc59336f7ea7e6b.png)
![f(x) = \frac{\sqrt[]{3}}{\sqrt[]{x^5}} f(x) = \frac{\sqrt[]{3}}{\sqrt[]{x^5}}](/latexrender/pictures/9b9aa23ebd46de8c990d06caa4d3369e.png)
![f(x) = \frac{\sqrt[]{3}}{x^{\frac{5}{2}}} f(x) = \frac{\sqrt[]{3}}{x^{\frac{5}{2}}}](/latexrender/pictures/6d903c691ac8f7912b2bb7730ac4a965.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jhonniewalk » Qui Mai 24, 2012 20:32
por jhonniewalk » Qui Mai 24, 2012 20:32
Obrigado pela ajuda. Estou a tentar mas não vai lá.
![f(x)=\frac{\sqrt[]{3}}{{x}^{\frac{5}{2}}} f(x)=\frac{\sqrt[]{3}}{{x}^{\frac{5}{2}}}](/latexrender/pictures/a7fe70ed13adb53b11e63c4e273e8291.png)
=
![\frac{\left(\sqrt[]{3} \right)\left({x}^{\frac{5}{2}}\right)-\left(\sqrt[]{3} \right)\left({x}^{\frac{5}{2}} \right)}{\left( {{x}^{\frac{5}{2}}} \right)^{2}} \frac{\left(\sqrt[]{3} \right)\left({x}^{\frac{5}{2}}\right)-\left(\sqrt[]{3} \right)\left({x}^{\frac{5}{2}} \right)}{\left( {{x}^{\frac{5}{2}}} \right)^{2}}](/latexrender/pictures/19fcd510e9d8a56b089ccd2d2d2dd535.png)
=
![-\frac{\sqrt[]{3}*\frac{5}{2}{x}^{\frac{3}{2}}}{{x}^{\frac{10}{2}}} -\frac{\sqrt[]{3}*\frac{5}{2}{x}^{\frac{3}{2}}}{{x}^{\frac{10}{2}}}](/latexrender/pictures/2bebc543dd7855b63fd2ebcde4b9fbab.png)
=
![\frac{\sqrt[]{3}*\frac{5}{2}\sqrt[]{{x}^{3}}}{{x}^{5}} \frac{\sqrt[]{3}*\frac{5}{2}\sqrt[]{{x}^{3}}}{{x}^{5}}](/latexrender/pictures/e3513e345066abbb46cdc92c2eb1e394.png)
Não estou a conseguir perceber o que me falta.
-
jhonniewalk
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mai 24, 2012 15:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecanica
- Andamento: cursando
 por DanielFerreira » Qui Mai 24, 2012 21:24
por DanielFerreira » Qui Mai 24, 2012 21:24
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jhonniewalk » Seg Mai 28, 2012 21:01
por jhonniewalk » Seg Mai 28, 2012 21:01
Obrigado,
Ajudou bastante

Mas seria mais fácil se tivesse convertido para a forma equivalente:
![\sqrt[]{3} * {x}^{-\frac{5}{2}} \sqrt[]{3} * {x}^{-\frac{5}{2}}](/latexrender/pictures/69b4ba8659270963c7d7f3a5bdfeff87.png)
Depois era só aplicar a regra do expoente.
Mais uma vez obrigado.
-
jhonniewalk
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mai 24, 2012 15:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecanica
- Andamento: cursando
 por DanielFerreira » Qui Mai 31, 2012 22:26
por DanielFerreira » Qui Mai 31, 2012 22:26
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Ajuda com calculo de derivada
por alienpuke » Sáb Out 24, 2015 15:45
- 2 Respostas
- 6988 Exibições
- Última mensagem por Cleyson007

Sáb Out 24, 2015 16:12
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda em Derivada
por vinim » Qua Jun 02, 2010 21:20
- 1 Respostas
- 1341 Exibições
- Última mensagem por MarceloFantini

Qui Jun 03, 2010 03:46
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Ajuda
por Bruna Cintra » Ter Mai 29, 2012 10:44
- 1 Respostas
- 1217 Exibições
- Última mensagem por Jhonata

Ter Mai 29, 2012 11:15
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - Ajuda?
por iceman » Ter Set 18, 2012 18:08
- 4 Respostas
- 2059 Exibições
- Última mensagem por iceman

Ter Set 18, 2012 18:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)= \sqrt[]{\frac{3}{{x}^{5}}} f(x)= \sqrt[]{\frac{3}{{x}^{5}}}](/latexrender/pictures/6ece9ac4538bf0ea0bb303ed33d0a445.png)
![f(x)=\frac{-5\sqrt[]{3}}{2\sqrt[]{{x}^{7}}} f(x)=\frac{-5\sqrt[]{3}}{2\sqrt[]{{x}^{7}}}](/latexrender/pictures/fa5b5f0eb3f6ee8718cb2ba5438439dd.png)
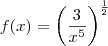 =
= 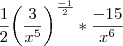 =
= ![\frac{1}{2\sqrt[]{}\frac{3}{{x}^{5}}}*\frac{-15}{{x}^{6}} \frac{1}{2\sqrt[]{}\frac{3}{{x}^{5}}}*\frac{-15}{{x}^{6}}](/latexrender/pictures/bffa052dc06a03638d03d8e1ec095f83.png) =
= ![\frac{-15}{2 {x}^{6}\sqrt[]{}\frac{3}{{x}^{5}}} \frac{-15}{2 {x}^{6}\sqrt[]{}\frac{3}{{x}^{5}}}](/latexrender/pictures/57bf6c56f7959b40bc1afbebbe32f813.png)


![f(x) = \sqrt[]{\frac{3}{x^5}} f(x) = \sqrt[]{\frac{3}{x^5}}](/latexrender/pictures/9736ee344761b5f3cbc59336f7ea7e6b.png)
![f(x) = \frac{\sqrt[]{3}}{\sqrt[]{x^5}} f(x) = \frac{\sqrt[]{3}}{\sqrt[]{x^5}}](/latexrender/pictures/9b9aa23ebd46de8c990d06caa4d3369e.png)
![f(x) = \frac{\sqrt[]{3}}{x^{\frac{5}{2}}} f(x) = \frac{\sqrt[]{3}}{x^{\frac{5}{2}}}](/latexrender/pictures/6d903c691ac8f7912b2bb7730ac4a965.png)

![f(x)=\frac{\sqrt[]{3}}{{x}^{\frac{5}{2}}} f(x)=\frac{\sqrt[]{3}}{{x}^{\frac{5}{2}}}](/latexrender/pictures/a7fe70ed13adb53b11e63c4e273e8291.png) =
= ![\frac{\left(\sqrt[]{3} \right)\left({x}^{\frac{5}{2}}\right)-\left(\sqrt[]{3} \right)\left({x}^{\frac{5}{2}} \right)}{\left( {{x}^{\frac{5}{2}}} \right)^{2}} \frac{\left(\sqrt[]{3} \right)\left({x}^{\frac{5}{2}}\right)-\left(\sqrt[]{3} \right)\left({x}^{\frac{5}{2}} \right)}{\left( {{x}^{\frac{5}{2}}} \right)^{2}}](/latexrender/pictures/19fcd510e9d8a56b089ccd2d2d2dd535.png) =
= ![-\frac{\sqrt[]{3}*\frac{5}{2}{x}^{\frac{3}{2}}}{{x}^{\frac{10}{2}}} -\frac{\sqrt[]{3}*\frac{5}{2}{x}^{\frac{3}{2}}}{{x}^{\frac{10}{2}}}](/latexrender/pictures/2bebc543dd7855b63fd2ebcde4b9fbab.png) =
= ![\frac{\sqrt[]{3}*\frac{5}{2}\sqrt[]{{x}^{3}}}{{x}^{5}} \frac{\sqrt[]{3}*\frac{5}{2}\sqrt[]{{x}^{3}}}{{x}^{5}}](/latexrender/pictures/e3513e345066abbb46cdc92c2eb1e394.png)
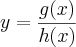
![f'(x) = \frac{g'(x).h(x) - g(x).h'(x)}{[h(x)]^2} f'(x) = \frac{g'(x).h(x) - g(x).h'(x)}{[h(x)]^2}](/latexrender/pictures/a029df2b00c3772431e006c0869d1ed8.png)
![g(x) = \sqrt[]{3} =====> g'(x) = 0 g(x) = \sqrt[]{3} =====> g'(x) = 0](/latexrender/pictures/771cf72235012990685b173d5f3c03d4.png)

![f'(x) = \frac{0 . x^{\frac{5}{2}} - \sqrt[]{3}.\frac{5}{2}.x^{\frac{3}{2}}}{(x^{\frac{5}{2}})^2} f'(x) = \frac{0 . x^{\frac{5}{2}} - \sqrt[]{3}.\frac{5}{2}.x^{\frac{3}{2}}}{(x^{\frac{5}{2}})^2}](/latexrender/pictures/220ab2fd2dfd6c5d8c0743c3aaac63d0.png)
![f'(x) = - \frac{\sqrt[]{3}.\frac{5}{2}.x^{\frac{3}{2}}}{x^5} f'(x) = - \frac{\sqrt[]{3}.\frac{5}{2}.x^{\frac{3}{2}}}{x^5}](/latexrender/pictures/accaacde70b7803734b9b9168dbc9b3f.png)
![f'(x) = - \sqrt[]{3} . \frac{5}{2} . x^{- \frac{7}{2}} f'(x) = - \sqrt[]{3} . \frac{5}{2} . x^{- \frac{7}{2}}](/latexrender/pictures/230822e601ad780e8d287be2238630a2.png)
![f'(x) = \frac{- 5\sqrt[]{3}}{2}. \frac{1}{x^{\frac{7}{2}}} f'(x) = \frac{- 5\sqrt[]{3}}{2}. \frac{1}{x^{\frac{7}{2}}}](/latexrender/pictures/a8c1f43a4b405ce3e2b1425211c3b893.png)
![f'(x) = \frac{- 5\sqrt[]{3}}{2\sqrt[]{x^7}}} f'(x) = \frac{- 5\sqrt[]{3}}{2\sqrt[]{x^7}}}](/latexrender/pictures/e852d912780e6b83febd94ef1d54d5fd.png)

![\sqrt[]{3} * {x}^{-\frac{5}{2}} \sqrt[]{3} * {x}^{-\frac{5}{2}}](/latexrender/pictures/69b4ba8659270963c7d7f3a5bdfeff87.png)
