 por alisson_bueno » Ter Mai 08, 2012 23:25
por alisson_bueno » Ter Mai 08, 2012 23:25
Ola a todos do forum,sou novo aqui e estou com dúvidas sobre como resolver a seguinte função:
Dada a função f(X),determine a derivada: f(X)=ln X/?x
Estou aprofundando regra da cadeia,mais como tenho prova daqui uns dias,estou revisando a matéria,e não sei como resolver este problema.
Alguem poderia resolve-la detalhadamente?
-
alisson_bueno
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mai 08, 2012 22:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em ciências economicas
- Andamento: cursando
 por DanielFerreira » Ter Mai 08, 2012 23:39
por DanielFerreira » Ter Mai 08, 2012 23:39
E aí
Alisson, blz?
seja bem vindo!!
![f(x) = \frac{ln x}{\sqrt[]{x}} f(x) = \frac{ln x}{\sqrt[]{x}}](/latexrender/pictures/b43acae8999771d8ef7ca3fb8879e227.png)
![f'(x) = \frac{\frac{1}{x}.\sqrt[]{x} - ln x . \frac{1}{2}.x^{- \frac{1}{2}}}{(\sqrt[]{x})^2} f'(x) = \frac{\frac{1}{x}.\sqrt[]{x} - ln x . \frac{1}{2}.x^{- \frac{1}{2}}}{(\sqrt[]{x})^2}](/latexrender/pictures/26f3eca6e3d3de2761c87223a51006ab.png)
![f'(x) = \frac{\frac{\sqrt[]{x}}{x} - \frac{ln x}{2\sqrt[]{x}}}{x} f'(x) = \frac{\frac{\sqrt[]{x}}{x} - \frac{ln x}{2\sqrt[]{x}}}{x}](/latexrender/pictures/c5ca979334fe33f51d7d4285c594e719.png)
Até aqui algo diferente do q vc fez??
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por alisson_bueno » Qua Mai 09, 2012 14:48
por alisson_bueno » Qua Mai 09, 2012 14:48
utilizei esse raciocinio:passei a raiz multiplicando ,ficando da seguinte maneira lnx*x^1/2.Como proceder agora?
Esqueci de mencionar que o resultado final é f'(X)=x^-3/2-1/2x^-3/2.lnx.
-
alisson_bueno
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mai 08, 2012 22:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em ciências economicas
- Andamento: cursando
 por DanielFerreira » Qua Mai 09, 2012 23:13
por DanielFerreira » Qua Mai 09, 2012 23:13
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por alisson_bueno » Qui Mai 10, 2012 22:19
por alisson_bueno » Qui Mai 10, 2012 22:19
Obrigado Danjr5,agora sei onde estava errando.
vlw cara!
-
alisson_bueno
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mai 08, 2012 22:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em ciências economicas
- Andamento: cursando
 por DanielFerreira » Qui Mai 10, 2012 22:21
por DanielFerreira » Qui Mai 10, 2012 22:21
Vlw.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 10502 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10708 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 12966 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14583 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 4969 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![f(x) = \frac{ln x}{\sqrt[]{x}} f(x) = \frac{ln x}{\sqrt[]{x}}](/latexrender/pictures/b43acae8999771d8ef7ca3fb8879e227.png)
![f'(x) = \frac{\frac{1}{x}.\sqrt[]{x} - ln x . \frac{1}{2}.x^{- \frac{1}{2}}}{(\sqrt[]{x})^2} f'(x) = \frac{\frac{1}{x}.\sqrt[]{x} - ln x . \frac{1}{2}.x^{- \frac{1}{2}}}{(\sqrt[]{x})^2}](/latexrender/pictures/26f3eca6e3d3de2761c87223a51006ab.png)
![f'(x) = \frac{\frac{\sqrt[]{x}}{x} - \frac{ln x}{2\sqrt[]{x}}}{x} f'(x) = \frac{\frac{\sqrt[]{x}}{x} - \frac{ln x}{2\sqrt[]{x}}}{x}](/latexrender/pictures/c5ca979334fe33f51d7d4285c594e719.png)

![f'(x) = \frac{\frac{\sqrt[]{x}.2.\sqrt[]{x}- x.lnx}{2x.\sqrt[]{x}}}{x} f'(x) = \frac{\frac{\sqrt[]{x}.2.\sqrt[]{x}- x.lnx}{2x.\sqrt[]{x}}}{x}](/latexrender/pictures/45f19986a5fbecfd875376beb1b362f0.png)
![f'(x) = \frac{\frac{2x - x.lnx}{2x\sqrt[]{x}}}{x} f'(x) = \frac{\frac{2x - x.lnx}{2x\sqrt[]{x}}}{x}](/latexrender/pictures/b9d2bd1672cae5da3614134425e6cdb0.png)
![f'(x) = \frac{x(2 - lnx)}{2x\sqrt[]{x}}:{x} f'(x) = \frac{x(2 - lnx)}{2x\sqrt[]{x}}:{x}](/latexrender/pictures/30b47b6ddea5020290a3ce3201cc9adf.png)
![f'(x) = \frac{2 - lnx}{2.\sqrt[]{x}}.\frac{1}{x} f'(x) = \frac{2 - lnx}{2.\sqrt[]{x}}.\frac{1}{x}](/latexrender/pictures/bfae49b0e503c2b958ae9982d2b2a598.png)
![f'(x) = \frac{2 - lnx}{2.\sqrt[]{x^3}} f'(x) = \frac{2 - lnx}{2.\sqrt[]{x^3}}](/latexrender/pictures/919a3879f708b991aecb93f53e8c721c.png)
![f'(x) = \frac{2}{2.\sqrt[]{x^3}} -\frac{lnx}{2.\sqrt[]{x^3}} f'(x) = \frac{2}{2.\sqrt[]{x^3}} -\frac{lnx}{2.\sqrt[]{x^3}}](/latexrender/pictures/c87771ca14f076c649a2c15f600118c9.png)
![f'(x) = \frac{1}{\sqrt[]{x^3}} -\frac{lnx}{2.\sqrt[]{x^3}} f'(x) = \frac{1}{\sqrt[]{x^3}} -\frac{lnx}{2.\sqrt[]{x^3}}](/latexrender/pictures/c5e10fb383c608b5818895117ae28a33.png)
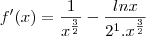
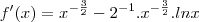
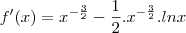


 , avisa que eu resolvo.
, avisa que eu resolvo.

