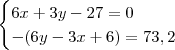a questão é a seguinte: Dois vértices de um triangulo são A(4,1) e B(10,4). Determine as coordenadas do terceiro ponto sabendo que a area é 36,6 e que o trinagulo é retangulo.
eu consegui fazer uma parte do exercicio:
AB * AC
(10-4)i + (4-1)j * (x-4)i + (y-1)j
6i*(x-4)i + 3j*(y-1)j
6x+3y-27 = 0 ---> primeira equação
resolve-se a matriz:
i j k
6 3 0
x-4 y-1 0, obtendo-se: k*(6y-6) - (3x - 12)
agora eu não consegui sair dai, sei que tem q elevar ao quadrado, mas nao sei por onde começar! me ajudeeem! esse trabalho é pra amanha, vale bem nota! :/
obrigada.


 .
.![\frac{1}{2}\sqrt{0^2 + 0^2 + [(6y-6) - (3x - 12)]^2} = 36,6 \frac{1}{2}\sqrt{0^2 + 0^2 + [(6y-6) - (3x - 12)]^2} = 36,6](/latexrender/pictures/35824b101ad2703700f4fe4831690814.png)