 por Cleyson007 » Qua Mar 07, 2012 17:27
por Cleyson007 » Qua Mar 07, 2012 17:27
Boa tarde amigos do Ajuda Matemática!
Nossa, estou com muita dificuldade em minhas aulas de Álgebra... Como resolver exercícios do tipo que seguem?
1°) Verifique que:
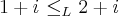
2°) Verifique que:
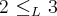
Alguém pode me ajudar?
Fico no aguardo.
Editado pela última vez por
Cleyson007 em Qua Mar 07, 2012 20:51, em um total de 1 vez.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qua Mar 07, 2012 18:54
por MarceloFantini » Qua Mar 07, 2012 18:54
Cleyson, você poderia por favor colocar o enunciado completo? O que é
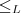
? O que é

? A segunda linha é uma conclusão da primeira? Está confuso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Qua Mar 07, 2012 20:50
por Cleyson007 » Qua Mar 07, 2012 20:50
Boa noite Marcelo!
O enunciado está completo!
O

significa o estudo lexicográfico no conjunto dos complexos; o

é a parte imaginária.
Cada linha é um exercício (editei para ficilitar a compreensão).
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qua Mar 07, 2012 21:05
por MarceloFantini » Qua Mar 07, 2012 21:05
Pelo enunciado, estou supondo que a ordem definida seja

se
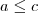
. Desta forma parece tranquilo, não? No segundo caso, teremos
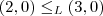
, logo
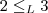
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dificuldade em Álgebra
por Rodrigo Ferreira » Dom Mar 11, 2012 20:44
- 1 Respostas
- 860 Exibições
- Última mensagem por LuizAquino

Seg Mar 12, 2012 12:27
Álgebra Elementar
-
- Dificuldade
por Alison Bissoli » Qui Dez 03, 2009 13:40
- 6 Respostas
- 3838 Exibições
- Última mensagem por Elcioschin

Dom Dez 06, 2009 13:54
Estatística
-
- Dificuldade
por Mauricio pelinson » Qui Fev 02, 2012 19:22
- 0 Respostas
- 4353 Exibições
- Última mensagem por Mauricio pelinson

Qui Fev 02, 2012 19:22
Sequências
-
- Dificuldade
 por Jhennyfer » Ter Jun 18, 2013 17:04
por Jhennyfer » Ter Jun 18, 2013 17:04
- 5 Respostas
- 5755 Exibições
- Última mensagem por jeniffer05

Dom Mai 11, 2014 15:32
Teoria dos Números
-
- Dificuldade resolução
 por Alvadorn » Sáb Fev 20, 2010 12:55
por Alvadorn » Sáb Fev 20, 2010 12:55
- 2 Respostas
- 1957 Exibições
- Última mensagem por Alvadorn

Dom Fev 21, 2010 16:32
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
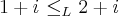
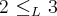

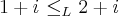
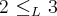

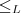 ? O que é
? O que é  ? A segunda linha é uma conclusão da primeira? Está confuso.
? A segunda linha é uma conclusão da primeira? Está confuso.

 significa o estudo lexicográfico no conjunto dos complexos; o
significa o estudo lexicográfico no conjunto dos complexos; o  é a parte imaginária.
é a parte imaginária.
 se
se 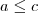 . Desta forma parece tranquilo, não? No segundo caso, teremos
. Desta forma parece tranquilo, não? No segundo caso, teremos 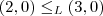 , logo
, logo 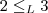 .
.
