 por Andrewo » Qui Jan 12, 2012 11:40
por Andrewo » Qui Jan 12, 2012 11:40
Olá pessoal, não sei se estou postando no lugar certo, se caso não esteja, algum moderador por favor mova o tópico.
Minha dúvida é a seguinte : Eu sei fazer contas simples pra descobrir o MMC e MDC, mas estava vendo uns problemas e não consegui resolver.São 3 questões:
1 - Se x é um número natural em que mmc(140,x)= 2100 e mdc(140,x)=10, podemos dizer que x :
(a)É um nº primo
(b)É um nº par
(c)É maior que 150
(d)É divisível por 11
(e)É múltiplo de 14
2 - Se x e y são números naturais em que MMC(y,x) =154 e MDC(y,x)=2, podemos dizer que cy:
(a)É um nº primo
(b)É um nº ímpar
(c)É maior que 500
(d)É divisível por 11
(e)É múltiplo de 15
3 - Se x e y são nº naturais em que MMC(y,x)=115 e MDC(y,x)=214, podemos dizer que o resto da divisão de xy por 107 é:
(a)Nº primo
(b)Nº par
(C)Nº maior que 100
(d)É 214
(e)É 115a
Não consigo resolver, talvez exista alguma propriedade pra fazer a conta?
-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por ant_dii » Qui Jan 12, 2012 12:07
por ant_dii » Qui Jan 12, 2012 12:07
Bom dia.
Para cada um dos exercícios abaixo você poderá usar a relação
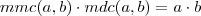
Mas ficou confuso os enunciados
Andrewo escreveu:2 - Se x e y são números naturais em que MMC(y,x) =154 e MDC(y,x)=2, podemos dizer que cy:
este o problema é quem é esse
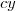
, não seria
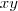
. Caso seja como eu disse, use a relação acima e saberá a resposta.
E
Andrewo escreveu:3 - Se x e y são nº naturais em que MMC(y,x)=115 e MDC(y,x)=214, podemos dizer que o resto da divisão de xy por 107 é:
(a)Nº primo
(b)Nº par
(C)Nº maior que 100
(d)É 214
(e)É 115a[/b]
Neste o problema é que a resposta pode ser é um nº par, é maior que 100, mas resta saber se na opção da letra e) esse 115a indica um múltiplo de 115, se o for, essa é a opção correta, mas verifique o enunciado.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Arkanus Darondra » Qui Jan 12, 2012 12:31
por Arkanus Darondra » Qui Jan 12, 2012 12:31
Concordo com o ant_dii.
Só que como na questão número 3 ele pergunta sobre o resto (= 0) e não sobre o quociente (= 230), a resposta seria a letra B.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por ant_dii » Qui Jan 12, 2012 12:47
por ant_dii » Qui Jan 12, 2012 12:47
Arkanus Darondra escreveu:Concordo com o ant_dii.
Só que como na questão número 3 ele pergunta sobre o resto (= 0) e não sobre o quociente (= 230), a resposta seria a letra B.
Concordo Arkanus... Não me atentei ao enunciado todo, olhei as alternativas e fiquei curioso sobre 115a... Desculpem-me.
Valewww...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Andrewo » Qui Jan 12, 2012 17:23
por Andrewo » Qui Jan 12, 2012 17:23
ant_dii escreveu:Arkanus Darondra escreveu:Concordo com o ant_dii.
Só que como na questão número 3 ele pergunta sobre o resto (= 0) e não sobre o quociente (= 230), a resposta seria a letra B.
Concordo Arkanus... Não me atentei ao enunciado todo, olhei as alternativas e fiquei curioso sobre 115a... Desculpem-me.
Valewww...
Peço desculpas AÍ, parceiros, eu errei na hora de digitar, não é 115a e sim só 115. E de fato a resposta é B
Obrigado pela ajuda.
Só mais uma coisa : como eu leio esse enunciado? -
a multiplicação de mmc e mmc é igual à multiplicação dos produtos? 
-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por ant_dii » Sex Jan 13, 2012 00:21
por ant_dii » Sex Jan 13, 2012 00:21
Lê-se "O produto do mínimo multiplo comum com o máximo divisor comum de dois números é igual ao produto dos dois números"...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


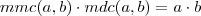
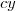 , não seria
, não seria 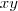 . Caso seja como eu disse, use a relação acima e saberá a resposta.
. Caso seja como eu disse, use a relação acima e saberá a resposta.






