 por nathyn » Qua Nov 16, 2011 14:36
por nathyn » Qua Nov 16, 2011 14:36
seja f(x) a função que associa a cada número real x, o menor dos números (x+1) e (-x+5). Então, o valor máximo de f(x) é:
a)1 b)3 c)4 d)5 e)7
A única forma que eu consegui resolver foi pegando as respostas e substituindo na equaçao, ex:
x+1=1
x=0
-x+5=1
x=4
Para o valor 3 foi a unica que encotrei o msmo x nas 2 respostas, por isso sei q essa eh a resposta...
x+1=3
x=2
-x+5=3
x=2
Mas sei tbm q nao eh dessa forma que se resolve... me ajudem ae por favor.
Obrigada.
Editado pela última vez por
nathyn em Qua Nov 16, 2011 21:33, em um total de 1 vez.
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Neperiano » Qua Nov 16, 2011 15:49
por Neperiano » Qua Nov 16, 2011 15:49
Ola
Até tem um outro jeito para resolver, se não me engano tenque usar derivada para achar valor maximo e minimo
Mas você pode fazer desse jeito que você resolveu, não tem problema fazer isso
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por nathyn » Qua Nov 16, 2011 21:34
por nathyn » Qua Nov 16, 2011 21:34
Po, brigada, mas eu queria mesmo a resolução caso eu não tivesse alternativas pra marcar...
Mas obrigada =)
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Nov 17, 2011 14:05
por MarceloFantini » Qui Nov 17, 2011 14:05
O Neperiano está enganado, não é necessário usar derivada. Perceba que conforme a variável x aumenta, o valor de

aumenta e

diminui. A função assume o menor dentre esses dois valores, então por exemplo para x=6 teremos
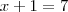
e
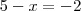
e a função teria valor
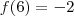
. Para x=-2, teríamos
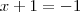
e
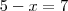
, logo
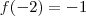
.
Assim, perceba que precisamos encontrar um valor de x que seja comum para ambas, pois então não há mínimo. Faça
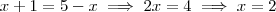
, daí
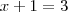
e
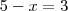
e finalmente
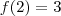
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nathyn » Seg Nov 21, 2011 10:41
por nathyn » Seg Nov 21, 2011 10:41
Pooxaa, brigadaãoo.
Questão facin...
Brigada msmo -)
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função] isso é função do segundo grau?
por maulakalanata » Qua Mar 27, 2013 04:03
- 1 Respostas
- 2169 Exibições
- Última mensagem por timoteo

Qua Mar 27, 2013 10:51
Funções
-
- [Função 1°grau] determinar função.
por Thiago 86 » Ter Abr 23, 2013 11:27
- 2 Respostas
- 2280 Exibições
- Última mensagem por Thiago 86

Ter Abr 23, 2013 13:05
Funções
-
- Função do 2° Grau
por mimi2009 » Qua Jun 10, 2009 05:46
- 1 Respostas
- 1987 Exibições
- Última mensagem por Molina

Qua Jun 10, 2009 08:05
Funções
-
- Função do 2 grau...
por Fiel8 » Qua Jul 01, 2009 21:34
- 4 Respostas
- 3306 Exibições
- Última mensagem por Cleyson007

Qui Jul 02, 2009 16:16
Funções
-
- Função 1° grau
por DanielFerreira » Ter Set 22, 2009 14:14
- 2 Respostas
- 2049 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 19:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 aumenta e
aumenta e  diminui. A função assume o menor dentre esses dois valores, então por exemplo para x=6 teremos
diminui. A função assume o menor dentre esses dois valores, então por exemplo para x=6 teremos 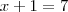 e
e 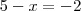 e a função teria valor
e a função teria valor 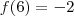 . Para x=-2, teríamos
. Para x=-2, teríamos 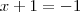 e
e 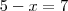 , logo
, logo 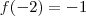 .
. 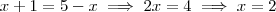 , daí
, daí 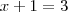 e
e 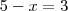 e finalmente
e finalmente 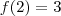 .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

