Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por joaofonseca » Seg Nov 14, 2011 22:13
por joaofonseca » Seg Nov 14, 2011 22:13
Sejam dois números positivos a e b cuja soma é 120. Qual o produto máximo que se pode obter entre metade de um e o quadrado do outro?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Neperiano » Qua Nov 16, 2011 15:45
por Neperiano » Qua Nov 16, 2011 15:45
Ola
a+b=120
a/2.2b=x
Minha sugestão é ir tentando valores de a e b, vá tentando a =0 b=120 e diminuindo até chegar 60 por 60, pegue numeros no meio aleatorioes só para ver e vá tentando
Deve ter uma outra forma de achar ela exata, talvez derivando, mas não sei como, vamos deixar aqui, se alguem souber
Mas eu tentaria por tentativa e erro
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por pedroaugustox47 » Sex Mai 11, 2012 17:17
por pedroaugustox47 » Sex Mai 11, 2012 17:17
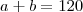
M.A (a,b)=
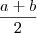
aplicando MA

MG temos:
60

![\sqrt[2]{a.b} \sqrt[2]{a.b}](/latexrender/pictures/b1aa488d7bbf6b51065de9b7abf15bfd.png)
3600

a.b
se queremos
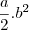
máximo, temos que ter a.b máximo
a.b máximo = 3600
temos o sistema
a+b=120
a.b+3600
logo a=60 e b =60

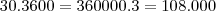
abraços

-
pedroaugustox47
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Mai 11, 2012 01:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Sistema Elite de Ensino-CN/EPCAR
- Andamento: cursando
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4948 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- Máximo e mínimo
por thadeu » Qua Nov 18, 2009 13:47
- 1 Respostas
- 4168 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 17:50
Trigonometria
-
- máximo da função
por David Soni » Qua Nov 25, 2009 10:04
- 0 Respostas
- 1580 Exibições
- Última mensagem por David Soni

Qua Nov 25, 2009 10:04
Trigonometria
-
- Lucro máximo
por Dih » Dom Mar 27, 2011 01:43
- 2 Respostas
- 2504 Exibições
- Última mensagem por Dih

Qui Mar 31, 2011 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Maximo e Minimo]
por Scheu » Sex Mar 16, 2012 01:23
- 1 Respostas
- 2468 Exibições
- Última mensagem por MarceloFantini

Sex Mar 16, 2012 03:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




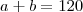
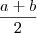
 MG temos:
MG temos:
![\sqrt[2]{a.b} \sqrt[2]{a.b}](/latexrender/pictures/b1aa488d7bbf6b51065de9b7abf15bfd.png)
 a.b
a.b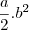 máximo, temos que ter a.b máximo
máximo, temos que ter a.b máximo
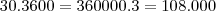


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)