a(
 vezes alguma coisa + algum termo independente) +b(
vezes alguma coisa + algum termo independente) +b(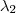 vezes alguma coisa + algum termo independente)=0
vezes alguma coisa + algum termo independente)=0Onde a e b são os dois lados em função dos quais eu escrevi os outros vetores. Escolhendo a e b linearmente independentes, a única solução possível é quando os coeficientes de a e b são igual a 0. Depois disso, resolvo o sistema e calculo tudo o que eu precisar. No link da apostila abaixo, há algum exemplos.
O problema é que eu não consegui achar uma relação dessa para o exercício abaixo:
Dado um triângulo
 ABC e I um ponto interior ao triângulo. Passando por
ABC e I um ponto interior ao triângulo. Passando porI, traçamos os segmentos PQ, RS, TU paralelos respectivamente a AB, BC e CA respectivamente.
(Com os pontos P, S em AC, T,Q em BC e U, R em AB. Demonstre que:

Se quiser ver a figura, veja na página 32 dessa apostila http://gradmat.ufabc.edu.br/cursos/ga/n ... -Notas.pdf
Alguém pode me ajudar?


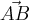 e
e 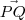 são paralelos, temos que
são paralelos, temos que 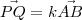 . Já que esses vetores possuem o mesmo sentido, então sabemos que
. Já que esses vetores possuem o mesmo sentido, então sabemos que 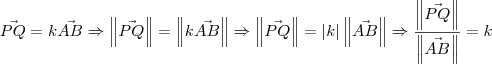
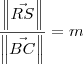
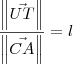
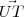 pois ele tem o mesmo sentido que
pois ele tem o mesmo sentido que  e portanto
e portanto  isso não interfere no que desejamos provar.
isso não interfere no que desejamos provar.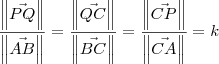
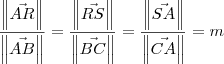
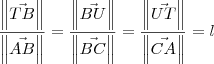
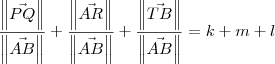
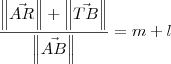
 . Dessa forma, temos que:
. Dessa forma, temos que: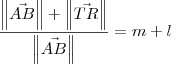
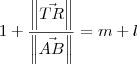
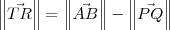 .
.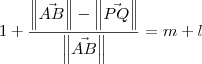


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)