Bom dia a todos,
Gosto muito de matemática e sempre tento conseguir fazer coisas novas com ajuda desta
ferramenta. Hávia visitado este site outras vezes para fazer consultas diversas, desta
vez resolvi me cadastrar pois não achei solução para a questão que vou propor. Sei
que o site pede para demostrarmos que tentamos resolver as questões para discuti-las,
em vez de termos só as respostas. Tentei de várias formas resolver o problema abaixo,
mas vou postar somente a última, que de todas a que tentei foi a mais "lúcida".
Segue:
A questão é isolar a variável "i" da equação \[c(\frac{i}{1-(1+i)^{-n}})=pmt\]
Fiz desta forma:
\[c=pmt-pmt\frac{1}{(1+i)^n}\]
\[c=pmt-\frac{pmt}{(1+i)^n}\]
\[c=\frac{pmt(1+i)^n-pmt}{(1+i)^n}\]
e travei aqui...
\[\frac {c(1+i)^n}{pmt}=-1+(1+i)^n\]
tentei fazer logarítmos e tentei encontrar através de raízes, mas sem sucesso.
Agradeço pela ajuda.
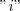
![\[c(\frac{i}{1-(1+i)^{-n}})=pmt\]
Fiz desta forma:
\[c=pmt-pmt\frac{1}{(1+i)^n}\]
\[c=pmt-\frac{pmt}{(1+i)^n}\]
\[c=\frac{pmt(1+i)^n-pmt}{(1+i)^n}\]
e travei aqui...
\[\frac {c(1+i)^n}{pmt}=-1+(1+i)^n\]](/latexrender/pictures/c32a9ed7bbf1b32cb4a8c6db470e4ea9.png "\[c(\frac{i}{1-(1+i)^{-n}})=pmt\]
Fiz desta forma:
\[c=pmt-pmt\frac{1}{(1+i)^n}\]
\[c=pmt-\frac{pmt}{(1+i)^n}\]
\[c=\frac{pmt(1+i)^n-pmt}{(1+i)^n}\]
e travei aqui...
\[\frac {c(1+i)^n}{pmt}=-1+(1+i)^n\]")
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)