Resposta:
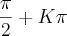
Nos meus calculo eu cheguei a rersposta cos(90°-x)= +- 1 Agora eu não consigo desenvolver..Agradeço muito quem desenvolver!

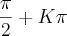

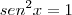
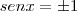



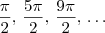 . Portanto uma primeira solução é
. Portanto uma primeira solução é 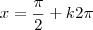 .
. 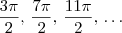 . A segunda solução é
. A segunda solução é 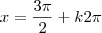 .
. 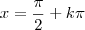 , lembrando que em todos os casos
, lembrando que em todos os casos  é qualquer número inteiro. Perceba que a forma condensada assume todos os valores das duas soluções encontradas anteriormente, e portanto é a mais elegante (e a que está no gabarito).
é qualquer número inteiro. Perceba que a forma condensada assume todos os valores das duas soluções encontradas anteriormente, e portanto é a mais elegante (e a que está no gabarito).

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.



