Inequação cujos denominadores são equações de 2º grau

por **Caroline Oliveyra** » Dom Jun 26, 2011 13:50

Olá!!
Mais uma vez eu aqui com essas equações... *-)

Enfim. Continuanado a minha querida lista de cálculo encontrei uma questão que é pra achar o conjunto solução da seguinte inequação:

$\frac{x}{x^2 - 5x + 6} + \frac{1}{2x} \geq \frac{2x}{x^2 - 4x + 3}$

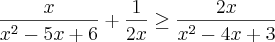
Eu comecei a resolver da seguinte forma: Primeiro multipliquei o numerador e o denominador de cada uma pelo denominador da outra para igualar os dois denominadores. Isso resultou na inequação

$\frac{2x^2}{2x^3 - 10x^2 + 12x} + \frac{x^2 - 5x +6}{2x^3 - 10x^2 + 12x} \geq \frac{2x}{x^2 - 4x + 3}$

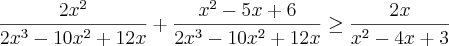
Somando as duas...

$\frac{3x^2 - 5x + 6}{x^3 - 5x^2 + 6x} \geq \frac{2x}{x^2 - 4x +6}$

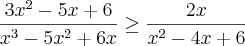
Depois disso eu multipliquei o primeiro membro pelo deniminador do segundo membro:

$\left(x^2 - 4x +3 \right). \frac{3x^2 - 5x + 6}{x^3 - 5x^2 + 6x} \geq 2x$

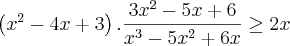
Multiplicando tudo no final deu isso aqui:

$\frac{3x^4 - 17x^3 + 35x^2 +18}{x^3 - 5x^2 + 6x} \geq 2x$

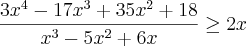
Ok, até aí tudo bem. Quando eu cheguei nesse ponto achei melhor simplificar primeiro essa fração pra depois somar o

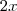, pra ficar menos complicado.
Então eu fatorei o termo independente da equação de 4º grau (numerador) e fui testando os números que apareceram na expressão. Encontrei que 1 é raiz. Então apliquei o dispositivo de Briot- Ruffini e encontrei a equação de 3º grau:

3x^3 - 14x^2 - 21x - 18

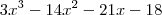
O que eu pretendia fazer agora era testar novamente os números que eu encontrei na fatoração (tanto os positivos quanto os negativos), já que o termo independente é o mesmo, e achar mais uma raiz pra eu poder aplicar Briot Ruffini de novo e chagar a uma equação de segundo grau. Dessa forma, eu encontraria as outras duas raizes e decomporia essa equação de 4º grau em uma de 1º grau: coef. do maior termo . $\left(x - {r}_{1} \right) . \left(x - {r}_{2} \right) . \left(x - {r}_{3} \right)$
Acontece que nessa equação de 3º grau que eu encontrei nenhum número que eu testei deu zero, ou seja, não consegui encontrar mais uma raiz.

Eu não sei como continuar... Não encontrar a raiz significa que a equação não tem raizes? Ou eu errei em algum lugar e não estou conseguindo perceber? E se a expressão não tem raizes como eu faço pra simplificar?

Grande beijo!! :-D

por **MarceloFantini** » Dom Jun 26, 2011 15:53

Caroline, você cometeu um erro comum ao trabalhar com inequações. Aqui está o seu erro:

$\frac{3x^2 -5x +6}{x^3 -5x^2 +6x} \geq \frac{2x}{x^2 -4x +6} \not\Rightarrow (x^2 -4x +3) \cdot \frac{3x^2 -5x +6}{x^3 -5x^2 +6x} \geq 2x$

Isso nem sempre é verdade, depende do valor de x! Portanto em problemas assim você tem que agrupar todas os termos de um único lado e analisar o sinal. Neste caso:

$\frac{3x^2 -5x +6}{x^3 -5x^2 +6x} - \frac{2x}{x^2 -4x+6} \geq 0$

Agora deixe tudo numa mesma fração e avalie onde a expressão é zero ou positiva.

Dica: ao invés de fazer os produtos como você fez no começo, encontre as raízes das frações originais e tornará tudo mais fácil.

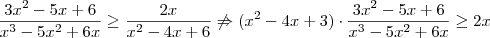
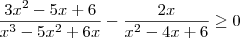
Um abraço.