 por Fabio Cabral » Ter Jun 07, 2011 10:41
por Fabio Cabral » Ter Jun 07, 2011 10:41
Veja:
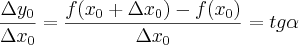
Vamos por partes.
Primeiro, queria entender
porque resulta em
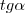
Segundo, isso é chamado de Razão Incremental?
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Claudin » Ter Jun 07, 2011 11:23
por Claudin » Ter Jun 07, 2011 11:23
Se for feito uma interpretação geométrica
você encontra a tangente no gráfico.
Recomendo a vídeo-aula do Luiz Aquino
http://www.youtube.com/watch?v=qbUTaeBG ... ideo_titleEditado pela última vez por
Claudin em Ter Jun 07, 2011 11:31, em um total de 1 vez.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Ter Jun 07, 2011 11:27
por LuizAquino » Ter Jun 07, 2011 11:27
Eu recomendo que você assista a
vídeo-aula "09. Cálculo I - Taxa de Variação". Ela aborda a sua primeira dúvida.
Quanto a segunda dúvida, esse quociente pode ser chamado de
razão incremental. Também é comum chamarmos de
taxa de variação.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Ter Jun 07, 2011 11:59
por Fabio Cabral » Ter Jun 07, 2011 11:59
Taxa de variação
instântanea? Usada para encontrar Reta Tangente?
Desculpe, mas não tenho acesso ao YouTube da aonde estou. Vou dar uma olhada mais tarde. Mas enquanto isso..
Veja essa afirmação:
"A derivada da função  , no ponto de abcissa x = 10 , sendo igual a 20, significa que a tangente trigonométrica da reta tangente à curva
, no ponto de abcissa x = 10 , sendo igual a 20, significa que a tangente trigonométrica da reta tangente à curva  , no ponto x = 10 , será também igual a 20."
, no ponto x = 10 , será também igual a 20."Significa que o angulo formado com o eixo das abscissas e pela reta Tangente tem valor 20?
Quero "interpretar" essa afirmação.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Ter Jun 07, 2011 12:13
por LuizAquino » Ter Jun 07, 2011 12:13
Fabio Cabral escreveu:"A derivada da função  , no ponto de abcissa x = 10 , sendo igual a 20, significa que a tangente trigonométrica da reta tangente à curva
, no ponto de abcissa x = 10 , sendo igual a 20, significa que a tangente trigonométrica da reta tangente à curva  , no ponto x = 10 , será também igual a 20."
, no ponto x = 10 , será também igual a 20."Significa que o angulo formado com o eixo das abscissas e pela reta Tangente tem valor 20?
Você deve entender melhor após assistir a vídeo aula.
O que isso significa é:
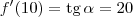
. Ou seja, o ângulo é
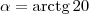
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Ter Jun 07, 2011 12:45
por MarceloFantini » Ter Jun 07, 2011 12:45
Evite enxergar como uma tangente e sim como um coeficiente angular.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- derivada! conceito!
por giulioaltoe » Qua Jul 20, 2011 09:43
- 4 Respostas
- 2802 Exibições
- Última mensagem por giulioaltoe

Qua Jul 20, 2011 12:54
Cálculo: Limites, Derivadas e Integrais
-
- Exercício teórico
por Cleyson007 » Sex Abr 27, 2012 12:28
- 4 Respostas
- 1731 Exibições
- Última mensagem por Guill

Sáb Abr 28, 2012 11:50
Cálculo: Limites, Derivadas e Integrais
-
- conceito de integral e limite
por OtavioBonassi » Sex Jan 07, 2011 15:52
- 11 Respostas
- 8704 Exibições
- Última mensagem por OtavioBonassi

Dom Jan 09, 2011 22:47
Cálculo: Limites, Derivadas e Integrais
-
- Conceito Formal de Limites
por mindy » Qua Abr 06, 2011 14:50
- 2 Respostas
- 3643 Exibições
- Última mensagem por mindy

Sex Abr 08, 2011 14:15
Cálculo: Limites, Derivadas e Integrais
-
- [Conceito correto de 3ª proporcional]
por Jhenrique » Qua Jul 25, 2012 02:51
- 1 Respostas
- 1208 Exibições
- Última mensagem por DanielFerreira

Dom Ago 05, 2012 16:20
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
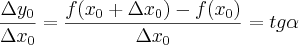
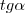

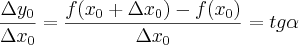
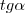



 , no ponto de abcissa x = 10 , sendo igual a 20, significa que a tangente trigonométrica da reta tangente à curva
, no ponto de abcissa x = 10 , sendo igual a 20, significa que a tangente trigonométrica da reta tangente à curva  , no ponto x = 10 , será também igual a 20."
, no ponto x = 10 , será também igual a 20."
, no ponto de abcissa x = 10 , sendo igual a 20, significa que a tangente trigonométrica da reta tangente à curva
, no ponto x = 10 , será também igual a 20."
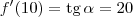 . Ou seja, o ângulo é
. Ou seja, o ângulo é 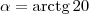 .
.


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.