 por Jhosmy » Qua Jun 01, 2011 15:14
por Jhosmy » Qua Jun 01, 2011 15:14
Por favor, dê uma olhada neste exercício.
Dados os Conjuntos A = {a,b,c} , B = {a,c,d,e} , C = {c,d} e D = {a,d,e} Classifique cada uma das sentenças seguintes em V (Verdadeira) ou F (Falsa)
a) A - B = {b} V, pois os únicos itens de A em comum com B são “a” e “c” ... restando apenas o “b” ...
b)Agora de uma olhada neste aqui... D – B = {c} Na resolução diz “F” , pois D – B = {a,e} e é diferente de {c}... Mais pensem... D está contido em B, quer dizer que todos os elementos de D estão em B... Não só isso mais D – B é { } conjunto vazio... e agora??
Editado pela última vez por
Jhosmy em Qua Jun 01, 2011 19:49, em um total de 1 vez.
-
Jhosmy
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Jun 01, 2011 15:06
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Nenhuma
- Andamento: cursando
 por carlosalesouza » Qua Jun 01, 2011 19:01
por carlosalesouza » Qua Jun 01, 2011 19:01
a) está correto... mas eu diria que A-B = {b} pois {b} é o conjunto de elementos de A que não estão em B
b) Concordo com o seu raciocínio... a afirmação continua sendo falsa... mas a resposta correta para D-B é

, como vc bem disse...
p = Livros são elaborados por pessoas
q = Pessoas cometem erros
r = Livros cometem erros
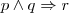
TAUTOLOGIA
UHuhahuauhahua
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Jhosmy » Qua Jun 01, 2011 19:21
por Jhosmy » Qua Jun 01, 2011 19:21
carlosalesouza escreveu:a) está correto... mas eu diria que A-B = {b} pois {b} é o conjunto de elementos de A que não estão em B
b) Concordo com o seu raciocínio... a afirmação continua sendo falsa... mas a resposta correta para D-B é

, como vc bem disse...
p = Livros são elaborados por pessoas
q = Pessoas cometem erros
r = Livros cometem erros
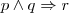
TAUTOLOGIA
UHuhahuauhahua
Um abraço
...Na alternatica " A " eu disse que era " b " !! ...
Grande Abraço...
-
Jhosmy
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Jun 01, 2011 15:06
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Nenhuma
- Andamento: cursando
 por carlosalesouza » Qui Jun 02, 2011 08:51
por carlosalesouza » Qui Jun 02, 2011 08:51
Como eu disse... sua resposta está correta...
Minha observação foi que eu expressaria a MESMA coisa de forma um tanto diferente...
Poderíamos, ainda, dizer que A - B é o complementar em A de

...
E estaríamos sempre dizendo a mesma coisa... rs
ok?
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Jhosmy » Sex Jun 03, 2011 22:43
por Jhosmy » Sex Jun 03, 2011 22:43
Não entendi muito bem, mais blza!.
^^
-
Jhosmy
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Jun 01, 2011 15:06
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Nenhuma
- Andamento: cursando
 por carlosalesouza » Sex Jun 03, 2011 23:56
por carlosalesouza » Sex Jun 03, 2011 23:56
Então vou resumir.... rs
O que eu quis mostrar, é que existem formas diferentes de afirmar a mesma verdade.... todas igualmente válidas...
Eu apenas mostrei certa preferência por afirmar de forma um pouco diferente da que vc afirmou... certo?
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Jhosmy » Sáb Jun 04, 2011 00:42
por Jhosmy » Sáb Jun 04, 2011 00:42
AH! sim.
Compreendi!
Obrigado.
-
Jhosmy
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Jun 01, 2011 15:06
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Nenhuma
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida sobre o conjunto VAZIO
por julianocarniel » Qui Mai 27, 2010 12:31
- 1 Respostas
- 1865 Exibições
- Última mensagem por 13run0

Sex Mai 28, 2010 15:20
Álgebra Elementar
-
- Dúvida sobre a resolução de um exercício
por Danilo » Qua Jul 25, 2012 12:15
- 1 Respostas
- 1404 Exibições
- Última mensagem por Danilo

Qua Jul 25, 2012 12:35
Álgebra Elementar
-
- [Probabilidade] Duvida sobre exercicio
por LsJack » Qui Ago 09, 2012 14:14
- 1 Respostas
- 1588 Exibições
- Última mensagem por fraol

Sáb Ago 11, 2012 12:34
Probabilidade
-
- Dúvida sobre resposta do exercício
por misaelbarreto » Dom Out 25, 2015 17:53
- 1 Respostas
- 1324 Exibições
- Última mensagem por misaelbarreto

Qui Out 29, 2015 00:44
Funções
-
- Exercício sobre equação da reta - Dúvida
 por Danilo » Seg Mai 07, 2012 00:28
por Danilo » Seg Mai 07, 2012 00:28
- 2 Respostas
- 1942 Exibições
- Última mensagem por Danilo

Dom Mai 13, 2012 22:38
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , como vc bem disse...
, como vc bem disse...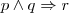 TAUTOLOGIA
TAUTOLOGIA
 ...
...