Dadas as seguintes sequências:
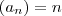
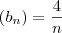
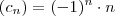
Calcule a ordem k para a qual os termos das diferentes sequências são iguais.
Pelo que entendi tem de se achar uma ordem k tal que
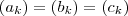 .
.Eu consegui resolver graficamente, com a ajuda da máquina. Mas como faço de forma algébrica?
Obrigado.


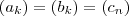 não seria
não seria 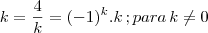



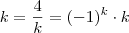
 então
então 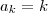 , similarmente se faz para o resto.
, similarmente se faz para o resto.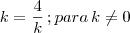
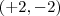 também servem para a segunda igualdade e desta forma temos como solução os dois,ou seja.
também servem para a segunda igualdade e desta forma temos como solução os dois,ou seja. é natural, então a única resposta válida é
é natural, então a única resposta válida é  .
.
