 por Abelardo » Sáb Abr 09, 2011 18:54
por Abelardo » Sáb Abr 09, 2011 18:54
58. Se x e y são números reais tais que x < y < 0, então é verdade que:
a)
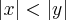
b)
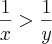
c)
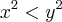
d)
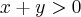
e)
![\sqrt[3]{x}> \sqrt[3]{y} \sqrt[3]{x}> \sqrt[3]{y}](/latexrender/pictures/354b75ab1de249142ce1449f42799ddb.png)
Como fazer??
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Fabricio dalla » Sáb Abr 09, 2011 19:42
por Fabricio dalla » Sáb Abr 09, 2011 19:42
cara eu acho que a letra b ta certa
chuta um valor pra y e x que atenda a condiçao de x < y <0
exp:
y=-4 e x=-20
-1/20 >-1/4 pois -0,05 esta + proximo de 0 e dos inteiros positivos do que -0,25
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
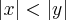
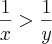
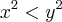
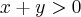
![\sqrt[3]{x}> \sqrt[3]{y} \sqrt[3]{x}> \sqrt[3]{y}](/latexrender/pictures/354b75ab1de249142ce1449f42799ddb.png)

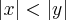
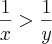
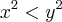
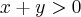
![\sqrt[3]{x}> \sqrt[3]{y} \sqrt[3]{x}> \sqrt[3]{y}](/latexrender/pictures/354b75ab1de249142ce1449f42799ddb.png)



 .
.
 :
: