olá pessoal, me ajuda nessa questão:
uma loja compra camisas de seda de $ 40,00 cada, revendendo-as por $ 70,00 a unidade. por este preço, foram vendidas mensalmente 60 camisas. a loja, para estimular a venda, pretende reduzir o preço das camisas. estima-se que para cada redução de $ 6,00, serão vendidas mais 15 camisas por mês. expresse a equação do lucro mensal e diga por quanto deve ser vendida a camisa para se ter um maior lucro possivel.
eu não sei bem por onde começar, ficaria grato se alguem me ajudasse explicando um passo-a-passo.


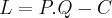 , onde P é o preço de cada unidade, Q é a quantidade de unidades, e C é o custo
, onde P é o preço de cada unidade, Q é a quantidade de unidades, e C é o custo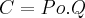 , com Po sendo o preço de compra.
, com Po sendo o preço de compra.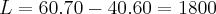
 e
e 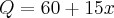 assim,
assim,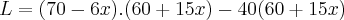



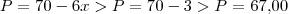




 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.