por Pedro123 » Ter Fev 22, 2011 20:55
por Pedro123 » Ter Fev 22, 2011 20:55
Galera, não consigo fazer essa questão de jeito nenhum, ve se alguem me da uma força abraços
(ITA - 1995) Considere C uma circunferência
centrada em O e raio 2r, e t a reta tangente a C num ponto T. Considere também A um ponto de C tal que AÔT =? é um ângulo agudo. Sendo B o ponto de t tal que o segmentoAB é paralelo ao segmento
OT, então a área do trapézio OABT é igual a:
(A) r²(2 cos? - cos 2?)
(B) 2r²(4 cos? - sen 2?)
(C) r²(4 sen? - sen 2?)
(D) r²(2 sen? + cos?)
(E) 2r²(2 sen 2? - cos 2?)
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por Renato_RJ » Ter Fev 22, 2011 22:55
por Renato_RJ » Ter Fev 22, 2011 22:55
Campeão, você teria a resposta ? Quero dizer, qual é a opção certa, pois fiz umas contas aqui e cheguei a um resultado, mas como geometria euclidiana não é a minha "praia", posso ter errado algo, e com o resultado posso postar a solução (ou não, se eu tiver errado), pois pensei assim:
Teremos um trapézio, a área do trapézio é
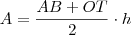
sendo h a altura do trapézio, sendo que OT = 2r.
AB seria a soma do trecho AK (sendo K o ponto de projeção de O no segmento AB) com 2r (projeção de OT no segmento AB), então para calcular h você teria que utilizar coseno de B, sendo
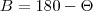
, para achar AK:
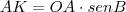
Então é só montar a equação da área com esses valores...
Abs,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Ter Fev 22, 2011 23:41
por LuizAquino » Ter Fev 22, 2011 23:41
A figura abaixo ilustra os dados do exercício.
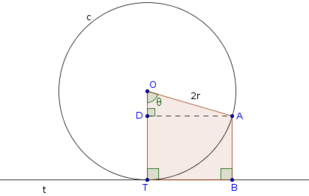
- ita-circulo.png (16.02 KiB) Exibido 2889 vezes
A área do trapézio será dada por
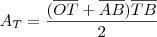
.
Facilmente determinamos que
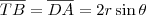
, usando o triângulo ODA.
Como
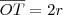
, falta determinar
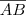
. Para isso, vamos aplicar o Teorema de Pitágoras no triângulos ODA (lembrando que

).
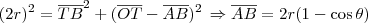
(fica como exercício desenvolver essa parte

)
Substituindo tudo para calcular a área:
}{2} = r^2(4-2\cos\theta)\sin\theta A_T = \frac{[2r + 2r(1-\cos\theta)](2r\sin\theta)}{2} = r^2(4-2\cos\theta)\sin\theta](/latexrender/pictures/be3b3ac1732a9c81eb074f1f5a297042.png)
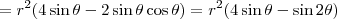
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Renato_RJ » Qua Fev 23, 2011 11:28
por Renato_RJ » Qua Fev 23, 2011 11:28
Luiz, cheguei ao mesmo resultado que você, mas fui por um lado mais complicado.. Hehehehe....
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Pedro123 » Qua Fev 23, 2011 20:49
por Pedro123 » Qua Fev 23, 2011 20:49
Valeu a todos galera, olha a besteira, tava fazendo o mais dificil, fazia tudo certo e esquecia de botar a area do triangulo dividida por 2 kkkkkkkk
mas muito obrigado a todos
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12994 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10976 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15117 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5034 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4803 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


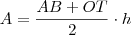 sendo h a altura do trapézio, sendo que OT = 2r.
sendo h a altura do trapézio, sendo que OT = 2r.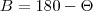 , para achar AK:
, para achar AK: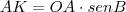

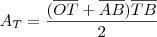 .
.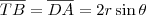 , usando o triângulo ODA.
, usando o triângulo ODA.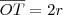 , falta determinar
, falta determinar 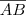 . Para isso, vamos aplicar o Teorema de Pitágoras no triângulos ODA (lembrando que
. Para isso, vamos aplicar o Teorema de Pitágoras no triângulos ODA (lembrando que  ).
).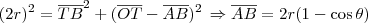 (fica como exercício desenvolver essa parte
(fica como exercício desenvolver essa parte  )
)}{2} = r^2(4-2\cos\theta)\sin\theta A_T = \frac{[2r + 2r(1-\cos\theta)](2r\sin\theta)}{2} = r^2(4-2\cos\theta)\sin\theta](/latexrender/pictures/be3b3ac1732a9c81eb074f1f5a297042.png)