Não consigo resolver de jeito nenhum esse exercicio:
[x]^1/2+[x+12]^1/2=6.
Tentei fazer elevando os dois lados ao quadrado mas assim tenho uma resposta diferente.
Grato se alguem me ajudar.



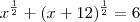
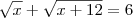
 para que não apareça a raiz de um número negativo. Já na segunda raiz, devemos ter
para que não apareça a raiz de um número negativo. Já na segunda raiz, devemos ter 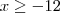 para que não apareça um número negativo dentro da raiz. Ora, sabemos que se x é um número tal que
para que não apareça um número negativo dentro da raiz. Ora, sabemos que se x é um número tal que  , então é verdade que
, então é verdade que 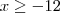 . Portanto, a solução dessa equação deve ser tal que
. Portanto, a solução dessa equação deve ser tal que  para que não apareça raízes de números negativos.
para que não apareça raízes de números negativos.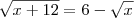
 , obtemos:
, obtemos: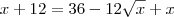
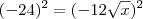

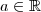 , então
, então 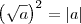 . Isto é, se você não sabe se o número a que está dentro da raiz é negativo ou positivo, então deve usar a simplificação
. Isto é, se você não sabe se o número a que está dentro da raiz é negativo ou positivo, então deve usar a simplificação 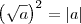 . Por outro lado, se você tem certeza que o número a é positivo, então pode fazer a simplificação
. Por outro lado, se você tem certeza que o número a é positivo, então pode fazer a simplificação 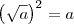 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.