Oi pessoal,
Sou novo no forum e sem grande experiência na área de matemática. Ultimamente me deparei com duas questões que não consigo nem "sair do canto". Espero que vocês possam me ajudar neste aspecto, visto que a probabilidade de uma destas ou as duas caírem na minha prova de Segunda-feira. Oo As questões estão nas imagens abaixo.
http://img522.imageshack.us/i/questo13.jpg/
http://img20.imageshack.us/i/questo30.jpg/
Por favor, me ajudem!



 .Temos:
.Temos:
 para o outro lado e o
para o outro lado e o  para o lado do
para o lado do 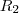 voce tera que a distancia de P aos centros e sempre uma constante que define uma hiperbole com foco nos centros das circunferencias.
voce tera que a distancia de P aos centros e sempre uma constante que define uma hiperbole com foco nos centros das circunferencias.
 ,teremos uma hipérbole pois os dois serão positivos ,pois:
,teremos uma hipérbole pois os dois serão positivos ,pois: e como
e como  é constante segue a definição de hipérbole.
é constante segue a definição de hipérbole. ou
ou .Teremos uma elipse e não importa qual vai ser menor os focos serão os mesmos e suas medidas também,pois:
.Teremos uma elipse e não importa qual vai ser menor os focos serão os mesmos e suas medidas também,pois:
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.