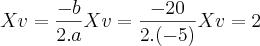por Marcos Paulo » Dom Nov 07, 2010 12:12
por Marcos Paulo » Dom Nov 07, 2010 12:12
Olá, estou com um problema na segiunte questao.. que estou estudando para uma prova.
# O Lucro de uma empresa é dado em função do Nº de peças produzidas (em milhares) L(x)= -x²+20x-30 , determine:
A) O lucro para se produzir 5 mil peças
b) O Nº de peças para se obter lucro máximo
C) O Lucro máximo
Eu não me recordo muito bem desta matéria, não estou sabendo o que fazer com o 5 mil da questão A e os procedimentos para as outras, que intendi é que como o A esta negativo o vertice da parabola é para baixo.. e o Xv= -b/2a e Yv= -delta/4a ,alguem pode me ajudar? Agradeço desde já, obrigado.
Para a letra B eu fiz
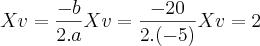
Para Letra C:

A letra não consegui, se poderem conferir as que eu fiz, ficaria agradecido to desesperado rsrs..
-
Marcos Paulo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Nov 07, 2010 11:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por JoaoGabriel » Dom Nov 07, 2010 14:55
por JoaoGabriel » Dom Nov 07, 2010 14:55
a) ele pede o L(5):
5² + 20 . 5 - 30
L(5) = 95
-
JoaoGabriel
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qua Ago 18, 2010 16:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudando para Engenharia Aeroespacial
- Andamento: cursando
 por Marcos Paulo » Dom Nov 07, 2010 14:57
por Marcos Paulo » Dom Nov 07, 2010 14:57
hmm.. saquei mas ai não tem que fazer nada de Xv e Yv do vertice? e a letra B e C, estao corretas?, mas entao seria.. obrigado
Editado pela última vez por
Marcos Paulo em Dom Nov 07, 2010 15:11, em um total de 1 vez.
-
Marcos Paulo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Nov 07, 2010 11:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por JoaoGabriel » Dom Nov 07, 2010 15:07
por JoaoGabriel » Dom Nov 07, 2010 15:07
eu so fiz a letra a) tenta fazer as outras
lembrando
xv = -b/2a
yv= - delta/4a
e não fica -5², pois qualquer numero elevado a expoente positivo vira positivo
ate mais
-

JoaoGabriel
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qua Ago 18, 2010 16:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudando para Engenharia Aeroespacial
- Andamento: cursando
 por Marcos Paulo » Dom Nov 07, 2010 15:12
por Marcos Paulo » Dom Nov 07, 2010 15:12
pod crer, nem lembrava.. ;x vou tentar aqui sim. vlw.
-
Marcos Paulo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Nov 07, 2010 11:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por Elcioschin » Dom Nov 07, 2010 22:39
por Elcioschin » Dom Nov 07, 2010 22:39
Infelizmente todas as soluções estão erradas
L(x) = - 5*x² + 20*x - 30
a) L(5) = - 5² + 20*5 - 30 ----> L(5) = - 25 + 100 - 30 ----> L(5) = 45
b) xV = - b/2a ----> a = - 1, b = 20 ----> xV = - 20/2*(-1) ----> xV = 10
c) yV = - 10² + 20*10 - 30 ----> yV = 70
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função(Calcular o x)
por alineasnovais » Sex Abr 26, 2013 19:04
- 3 Respostas
- 1461 Exibições
- Última mensagem por DanielFerreira

Sex Abr 26, 2013 21:28
Funções
-
- Calcular Função
por xafabi » Sex Mai 17, 2013 08:21
- 0 Respostas
- 774 Exibições
- Última mensagem por xafabi

Sex Mai 17, 2013 08:21
Cálculo: Limites, Derivadas e Integrais
-
- [Função Calcular f(2) e f(3)]
por ricardo de azevedo » Sex Ago 30, 2013 08:37
- 3 Respostas
- 4891 Exibições
- Última mensagem por e8group

Sex Ago 30, 2013 19:46
Funções
-
- Calcular periodos de uma funcao
por explod1ng » Sáb Mar 27, 2010 21:07
- 0 Respostas
- 1076 Exibições
- Última mensagem por explod1ng

Sáb Mar 27, 2010 21:07
Funções
-
- calcular a área da funçao
 por edilaine33 » Dom Dez 01, 2013 08:54
por edilaine33 » Dom Dez 01, 2013 08:54
- 1 Respostas
- 1709 Exibições
- Última mensagem por Pessoa Estranha

Dom Dez 01, 2013 10:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.