Seção para postagens de problemas matemáticos do cotidiano, reportagens, casos interessantes, polêmicos ou curiosos.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Gir » Seg Jul 27, 2009 11:46
por Gir » Seg Jul 27, 2009 11:46
O volume de um prisma regular de base quadrada é 700 cm³.O perimetro da base é de 40 cm.Calcule a altura e a área total do prisma.
40/2=20
A=l²
l²=20
V=Bh
700=40.h
h=35/2 cm
?
me ajudem!
700=40.h
-
Gir
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jul 02, 2009 17:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Seg Jul 27, 2009 15:35
por Molina » Seg Jul 27, 2009 15:35
Boa tarde, Gir.
Como a base é um quadrado e tem perímetro igual a 40cm, cada lado possui 10cm.
Utilizando os dados que temos agora, vamos calcular a altura do prisma:
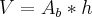
[volume é igual área da base vezes altura]
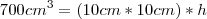
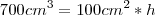
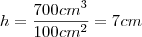
Agora pra descobrir a área total, você pode fazer um esboço deste prisma e "abri-lo" totalmente, de forma a deixa-lo no plano. E calcular cada área das figuras encontradas e soma-las.
Lembre-se que teremos
dois quadrados de 10cm de lado cada que são as bases do prisma; e
quatro retângulos de 10cm x 7cm cada que são os lados do prisma.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Gir » Ter Jul 28, 2009 13:36
por Gir » Ter Jul 28, 2009 13:36
obrigada!
A diagonal de um paralelepípedo reto retangular mede 20 raiz de 2 cm.As dimensoes desse paralelepípedo sao proporcionais aos numeros 5,4 e 3,respectivamente.Calcule as dimensoes desse paralelepipedo.(Faça a/5=b/4=c/3=k --> a=5k,b=4k,c=3k)
20 raiz de 2=raiz de (5k)²+(4k)²+(3k)²
.
.
.
k=5 raiz de 2/3
??
-
Gir
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jul 02, 2009 17:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Ter Jul 28, 2009 15:21
por Molina » Ter Jul 28, 2009 15:21
Gir escreveu:obrigada!
A diagonal de um paralelepípedo reto retangular mede 20 raiz de 2 cm.As dimensoes desse paralelepípedo sao proporcionais aos numeros 5,4 e 3,respectivamente.Calcule as dimensoes desse paralelepipedo.(Faça a/5=b/4=c/3=k --> a=5k,b=4k,c=3k)
20 raiz de 2=raiz de (5k)²+(4k)²+(3k)²
.
.
.
k=5 raiz de 2/3
??
Boa tarde, Gir.
Procure enunciar uma questão por tópico. Assim, outro usuário que tiver a mesma dúvida que você irá encontrá-la com mais facilidade..
Sobre a questão você precisa saber a fórmula da diagonal do paralelepípedo, que é:

, onde
a,
b e
c são os lados do paralelepípedo.
Desta forma:

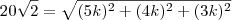
elevando ao quadrado de ambos os lados:



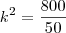


(lembrando que k = -4 é descartado)
Com isso temos que as dimensões são:
5k, 4k e 3k => 5*4, 4*4 e 3*4 => 20, 16 e 12.Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Problemas do Cotidiano
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2851 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6148 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
-
- Geometria espacial
por crixprof » Qui Out 15, 2009 10:40
- 2 Respostas
- 3158 Exibições
- Última mensagem por crixprof

Sex Out 16, 2009 18:27
Geometria Espacial
-
- Geometria Espacial
por geriane » Sáb Abr 03, 2010 10:39
- 4 Respostas
- 4202 Exibições
- Última mensagem por geriane

Dom Abr 04, 2010 10:29
Geometria Espacial
-
- Geometria espacial
por nayara michele » Ter Set 27, 2011 17:43
- 1 Respostas
- 2395 Exibições
- Última mensagem por Neperiano

Ter Set 27, 2011 18:02
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



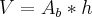 [volume é igual área da base vezes altura]
[volume é igual área da base vezes altura]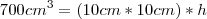
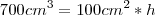
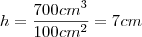



 , onde a, b e c são os lados do paralelepípedo.
, onde a, b e c são os lados do paralelepípedo.
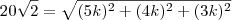



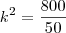

 (lembrando que k = -4 é descartado)
(lembrando que k = -4 é descartado)






