-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478674 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534540 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498110 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 713527 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2135280 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
Sub-seção para materiais das disciplinas relacionadas ao Instituto de Física.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Cleyson007 » Qui Dez 13, 2012 17:27
por Cleyson007 » Qui Dez 13, 2012 17:27
Vamos supor o corte pela metade de uma mola ideal sem massa. Considerando que a mola inteira possuia uma força constante k, qual é a constante de força de cada metade, em termos de k?
Resposta: 2k
E se fosse cortada em três partes iguais?
Resposta: 3k
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por fraol » Qui Dez 13, 2012 20:18
por fraol » Qui Dez 13, 2012 20:18
Olá
Cleyson007, boa noite.
Se a força elástica da mola é constante em todos os casos então:
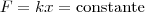
.
No caso de meia mola:
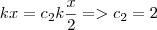
e portanto a nova constante é
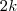
.
No caso de um terço de mola:

e portanto a nova constante é
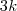
.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Cleyson007 » Qui Dez 13, 2012 21:19
por Cleyson007 » Qui Dez 13, 2012 21:19
Boa noite
Fraol!
Primeiramente, muito obrigado por ajudar.. Você é sempre muito solícito para comigo

Desculpe, mas eu não entendi.. Poderia explicar novamente?
Bom, o procedimento é análogo no caso da divisão em 3 partes. Explique-me a divisão em 2 partes.
Aguardo,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por fraol » Qui Dez 13, 2012 21:52
por fraol » Qui Dez 13, 2012 21:52
Olá,
Há casos de molas especiais em que a força se mantém constante numa determinada faixa de deslocamento ( exemplos: algumas molas em Y de aço inox, aquelas molas parabólicas, quase retas, dos caminhões e das antigas charretes, etc.). Aí a tal constante acaba variando


.
Então voltando ao problema e supondo que a força é constante então variando o deslocamento, variamos o tal k.
O que fiz, então foi supor
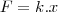
constante, assim quando temos deslocamento igual a x/2
=>
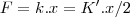
então
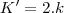
.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Cleyson007 » Sex Dez 14, 2012 10:00
por Cleyson007 » Sex Dez 14, 2012 10:00
Entendi

Obrigado!
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Física
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



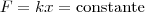 .
. 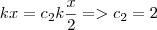 e portanto a nova constante é
e portanto a nova constante é 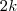 .
. e portanto a nova constante é
e portanto a nova constante é 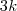 .
.
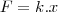 constante, assim quando temos deslocamento igual a x/2
constante, assim quando temos deslocamento igual a x/2 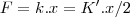 então
então 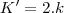 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)