-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477872 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529530 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493079 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 699090 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2109571 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
Sub-seção para materiais das disciplinas relacionadas ao Instituto de Física.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Cleyson007 » Qua Dez 12, 2012 17:59
por Cleyson007 » Qua Dez 12, 2012 17:59
A figura abaixo mostra o perfil JKLM de um tobogã, cujo trecho KLM é circular de centro em C e raio R = 5,4m. Uma criança de 15,0kg inicia sua descida, a partir do repouso, de uma altura h = 7,2m acima do plano horizontal que contém o centro C do trecho circular. Obs.: Considere os atritos desprezíveis e g = 10m/s².
Calcule a velocidade com que a criança passa pelo ponto L.
Estou fazendo assim:
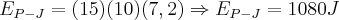
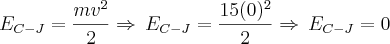
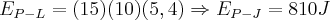

Pela conservação de energia:
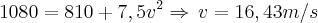 Gabarito
Gabarito:
v = 6m/sOnde estou errando?
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por fraol » Qua Dez 12, 2012 18:25
por fraol » Qua Dez 12, 2012 18:25
Observe as contas:
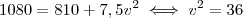
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Cleyson007 » Qua Dez 12, 2012 18:31
por Cleyson007 » Qua Dez 12, 2012 18:31
Desculpe Fraol, fiz tudo certo e esqueci de dividir por 7,5.
Já tinha quebrado a cabeça diversas vezes e não encontrava o meu erro.
Obrigado.
Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por fraol » Qua Dez 12, 2012 19:00
por fraol » Qua Dez 12, 2012 19:00
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Física
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Velocidade
por leticiapires52 » Dom Mar 08, 2015 14:09
- 1 Respostas
- 1812 Exibições
- Última mensagem por Russman

Seg Mar 09, 2015 03:02
Equações
-
- velocidade consatante
por vinicius reis » Sex Mar 18, 2011 15:21
- 1 Respostas
- 2089 Exibições
- Última mensagem por Renato_RJ

Sex Mar 18, 2011 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [VELOCIDADE ESCALAR!]
 por BARBARAF » Seg Jan 16, 2012 22:42
por BARBARAF » Seg Jan 16, 2012 22:42
- 1 Respostas
- 2859 Exibições
- Última mensagem por fraol

Ter Jan 17, 2012 13:41
Geometria Analítica
-
- Determinar a velocidade inicial
por alexandre32100 » Ter Mar 15, 2011 00:31
- 1 Respostas
- 2482 Exibições
- Última mensagem por Elcioschin

Ter Mar 15, 2011 14:38
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas - Velocidade e Aceleração
por Fabio Cabral » Ter Jun 14, 2011 14:49
- 1 Respostas
- 4049 Exibições
- Última mensagem por carlosalesouza

Ter Jun 14, 2011 15:40
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
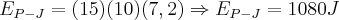
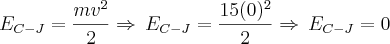
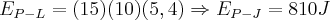

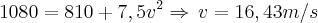

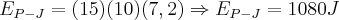
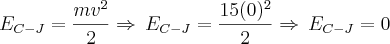
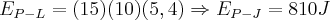

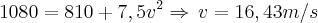

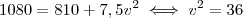





 , avisa que eu resolvo.
, avisa que eu resolvo.

