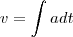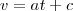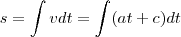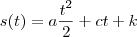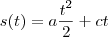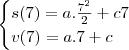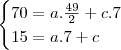Sub-seção para materiais das disciplinas relacionadas ao Instituto de Física.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Cleyson007 » Ter Out 30, 2012 11:08
por Cleyson007 » Ter Out 30, 2012 11:08
Resolva fazendo uso de integração.
Um antílope que se move com aceleração constante leva 7,0s para percorrer uma distância de 70,0m entre dois pontos. Ao passar pelo segundo ponto, sua velocidade é de 15,0m/s.
a) Qual era a sua velocidade quando passava pelo primeiro ponto? 5,0m/s
b) Qual era a sua aceleração? 1,43m/s²
Agradeço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por young_jedi » Ter Out 30, 2012 11:50
por young_jedi » Ter Out 30, 2012 11:50
sabendo que a aceleração é a derivada da velocidade, então a velocidade é a integral da aceleração
não sabemos a aceleração mais sabemos que ela é constante então dizemos que ele é a portanto a velocidade sera
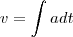
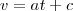
tambem sabemos que a velocidade é a derivada do deslocamento então
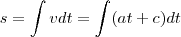
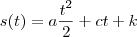
podemos considerar que inicialmente ele estava no ponto 0 ou seja s(0)=0
portanto temos
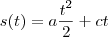
sabendo que no tempo de 7 s sua distancia sua posição é 70 m e sua velocidade é 15 m/s
então
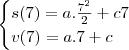
então
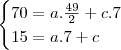
resolvendo este sistmea voce encontra as constantes a e c e determina a velocidae e o deslocamento.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Física
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integração por Partes] Constante de integração
por KleinIll » Dom Set 01, 2019 14:11
- 2 Respostas
- 5953 Exibições
- Última mensagem por KleinIll

Sex Set 06, 2019 18:39
Cálculo: Limites, Derivadas e Integrais
-
- [Limites de Integração] Como achar os limites de integração?
por Miine_J » Sáb Nov 10, 2018 03:13
- 2 Respostas
- 19681 Exibições
- Última mensagem por Miine_J

Dom Nov 11, 2018 08:17
Cálculo: Limites, Derivadas e Integrais
-
- Outra ED.
por Higor » Seg Fev 21, 2011 15:52
- 2 Respostas
- 1997 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 17:04
Cálculo: Limites, Derivadas e Integrais
-
- Outra - fração
por cidaiesbik » Qui Mai 21, 2009 10:35
- 3 Respostas
- 3572 Exibições
- Última mensagem por cidaiesbik

Seg Mai 25, 2009 10:17
Desafios Enviados
-
- Outra Dúvida
por rodsales » Sáb Jun 06, 2009 21:41
- 1 Respostas
- 1501 Exibições
- Última mensagem por Marcampucio

Sáb Jun 06, 2009 22:38
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.