Sub-seção para materiais das disciplinas relacionadas ao Instituto de Física.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Cleyson007 » Sex Jul 20, 2012 10:18
por Cleyson007 » Sex Jul 20, 2012 10:18
Bom dia a todos!
Demonstre a recíproca: se o movimento de uma partícula é dado por x = x0 + v(t - t0), então a velocidade média em qualquer intervalo de tempo é igual a v.
Tenho muita dificuldade com esses exercícios que pedem para demonstrar.. Se puder me ajudar, agradeço.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Arkanus Darondra » Sex Jul 20, 2012 10:43
por Arkanus Darondra » Sex Jul 20, 2012 10:43
Creio que seja assim:
Sabendo que a velocidade média é dada por
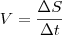
, vem:
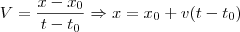
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Sex Jul 20, 2012 11:26
por Russman » Sex Jul 20, 2012 11:26
Ou então, de um parâmetro mais geral, a velocidade escalar média do trajeto da partícula é dada pela soma dos módulos das velocidades escalares em um numero finito de instantes dividido por este número. Ou seja,
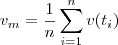
.
Como
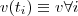
, então
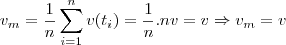
.
Agora, como assumimos
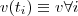
e
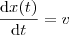
, então segue destas a equação do movimento.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Física
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Demonstração envolvendo ângulo
por Balanar » Qua Set 01, 2010 22:30
- 0 Respostas
- 1576 Exibições
- Última mensagem por Balanar

Qua Set 01, 2010 22:30
Geometria Plana
-
- Demonstração envolvendo bissetrizes
por Balanar » Qui Set 02, 2010 00:15
- 0 Respostas
- 1305 Exibições
- Última mensagem por Balanar

Qui Set 02, 2010 00:15
Geometria Plana
-
- Demonstração envolvendo triângulo
 por Balanar » Dom Out 17, 2010 00:47
por Balanar » Dom Out 17, 2010 00:47
- 3 Respostas
- 2061 Exibições
- Última mensagem por Balanar

Dom Out 17, 2010 21:09
Geometria Plana
-
- Demonstração envolvendo vetores
por VFernandes » Seg Mar 07, 2011 00:59
- 0 Respostas
- 2231 Exibições
- Última mensagem por VFernandes

Seg Mar 07, 2011 00:59
Geometria Plana
-
- Demonstração envolvendo bissetrizes (Confirmar)
por Balanar » Sex Set 03, 2010 19:52
- 0 Respostas
- 1136 Exibições
- Última mensagem por Balanar

Sex Set 03, 2010 19:52
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



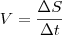 , vem:
, vem: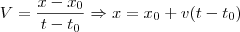
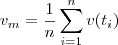 .
.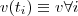 , então
, então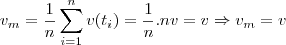 .
.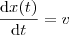 , então segue destas a equação do movimento.
, então segue destas a equação do movimento.
 .
.



