



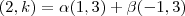 , ou seja, o vetor v seja combinação linear de u e w.
, ou seja, o vetor v seja combinação linear de u e w.
alzenir agapito escreveu:seja o conjunto de vetores { u= (1,3), v=(2,k), w=(-1,3)} qual é a condição sobre k para que este conjunto seja linearmente dependente.?
 (com m > n) é sempre L. D..
(com m > n) é sempre L. D..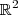 , para qualquer número real k temos que esse conjunto é L. D..
, para qualquer número real k temos que esse conjunto é L. D..



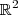 , ou seja, o espaço vetorial dos pares ordenados com coordenadas reais, é 2. Isso significa que qualquer conjunto com mais de 2 vetores de
, ou seja, o espaço vetorial dos pares ordenados com coordenadas reais, é 2. Isso significa que qualquer conjunto com mais de 2 vetores de 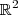 é, obrigatoriamente, linearmente dependente pois, caso contrário, esse espaço vetorial teria dimensão maior que dois, o que é um absurdo. Portanto, este conjunto será linearmente dependente para qualquer valor de k.
é, obrigatoriamente, linearmente dependente pois, caso contrário, esse espaço vetorial teria dimensão maior que dois, o que é um absurdo. Portanto, este conjunto será linearmente dependente para qualquer valor de k.

MarceloFantini escreveu:Alzenir, você não entendeu a resposta do Luiz Aquino. Note que a dimensão de, ou seja, o espaço vetorial dos pares ordenados com coordenadas reais, é 2. Isso significa que qualquer conjunto com mais de 2 vetores de
é, obrigatoriamente, linearmente dependente pois, caso contrário, esse espaço vetorial teria dimensão maior que dois, o que é um absurdo. Portanto, este conjunto será linearmente dependente para qualquer valor de k.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante