Entao pessoal, perdao pela minha ignorancia no assunto.
Mas meu objetivo é simples: Tenho duas curvas e quero medir a diferenca entre elas. Como nao tenho a funcao das curvas, nao posso medir a integral.
Mas tenho os pontos das curvas, entao fui sugerido a calcular o MSE. Beleza ate ai.
O mean squared error (MSE) no entanto necessita que eu calcule a diferenca de um ponto estimado (por uma funcao estimadora) e o ponto de cada uma das curvas.
Minha questao é? Como definir essa funcao estimadora? Essa informacao que eu nao consigo encontrar.
Se alguem puder ajudar eu agradeco.


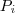 e a outra pelos pontos
e a outra pelos pontos 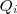 , com i=1, ..., N, sendo que eles seguem um mesmo sentido sobre o contorno das curvas. Uma forma bem simples de "medir" quão próximo uma curva está da outra é fazer:
, com i=1, ..., N, sendo que eles seguem um mesmo sentido sobre o contorno das curvas. Uma forma bem simples de "medir" quão próximo uma curva está da outra é fazer: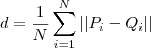

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)