Materiais sobre Geometria.
Utilize a seção de pedidos para outros que não estejam disponíveis.
As fontes dos arquivos serão diversas e deverão ser citadas sempre que possível, mantendo totalmente os créditos dos respectivos autores.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por andersontricordiano » Sáb Mar 26, 2011 18:21
por andersontricordiano » Sáb Mar 26, 2011 18:21
No triângulo isósceles ABC,sabendo que ângulo
B  C
C, a bissetriz
BD mede 6 cm e forma ângulo de 135° com o lado
AC , como mostra na figura . Calcule o comprimento do lado
ABA resposta é:

![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png)
isosceles.jpg.gif
OBRIGADO QUEM RESOLVER ESSE CALCULO!POR FAVOR RESOLVEM , EU JÁ TENTEI TODAS AS FORMULAS !!!!Você não está autorizado a ver ou baixar esse anexo.
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Pedro123 » Sáb Mar 26, 2011 22:33
por Pedro123 » Sáb Mar 26, 2011 22:33
ta ai a resolução meu caro, abraços
Temos que B=C=x
Veja que o angulo ADB mede 45°, agora veja que o angulo ABD mede x/2, e olhando para o triangulo ABC, temos que A = 180 -2x, portanto:
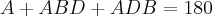
, logo -->
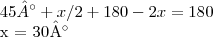
, logo
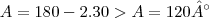
Podemos agora fazer a seguinte lei dos senos:
![AB/sen45° = 6/sen120° > AB /\sqrt[]{2}/2 = 6/\sqrt[]{3}/2 > AB = 6\sqrt[]{2} /\sqrt[]{3} AB/sen45° = 6/sen120° > AB /\sqrt[]{2}/2 = 6/\sqrt[]{3}/2 > AB = 6\sqrt[]{2} /\sqrt[]{3}](/latexrender/pictures/0fc6ad41439b9c4b84b918544cb076ba.png)
, que racionalizando temos:
![AB = 2\sqrt[]{6} AB = 2\sqrt[]{6}](/latexrender/pictures/e51ecabc862672843a7dd692d6de20a2.png)
.
Qualquer duvida pergunte abraços!
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por andersontricordiano » Dom Mar 27, 2011 13:07
por andersontricordiano » Dom Mar 27, 2011 13:07
obrigado Pedro!
Valeu!
Que Deus te abençoe!
Abraços!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- calcule o comprimento de uma circunferência...
por willwgo » Seg Mar 28, 2011 17:36
- 5 Respostas
- 5856 Exibições
- Última mensagem por marco brandao

Seg Mar 28, 2011 19:23
Geometria Plana
-
- Calcule o comprimento de uma circunferência de diâmetro d =
por Killder » Qua Nov 28, 2012 07:39
- 2 Respostas
- 5807 Exibições
- Última mensagem por Killder

Qua Nov 28, 2012 14:17
Cálculo: Limites, Derivadas e Integrais
-
- Triângulo isósceles
por DanielFerreira » Qua Jul 29, 2009 16:03
- 3 Respostas
- 9680 Exibições
- Última mensagem por DanielFerreira

Qui Jul 30, 2009 17:35
Geometria Plana
-
- Triângulo Isósceles
por DanielFerreira » Qui Mar 03, 2011 12:28
- 1 Respostas
- 2744 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 14:22
Geometria Plana
-
- triangulo isósceles
por alfabeta » Seg Mar 05, 2012 11:36
- 6 Respostas
- 4411 Exibições
- Última mensagem por alfabeta

Qui Mar 08, 2012 22:33
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 C, a bissetriz BD mede 6 cm e forma ângulo de 135° com o lado AC , como mostra na figura . Calcule o comprimento do lado AB
C, a bissetriz BD mede 6 cm e forma ângulo de 135° com o lado AC , como mostra na figura . Calcule o comprimento do lado AB
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png)

 C, a bissetriz BD mede 6 cm e forma ângulo de 135° com o lado AC , como mostra na figura . Calcule o comprimento do lado AB
C, a bissetriz BD mede 6 cm e forma ângulo de 135° com o lado AC , como mostra na figura . Calcule o comprimento do lado AB
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png)

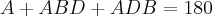 , logo -->
, logo --> 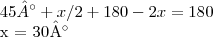 , logo
, logo 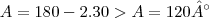
![AB/sen45° = 6/sen120° > AB /\sqrt[]{2}/2 = 6/\sqrt[]{3}/2 > AB = 6\sqrt[]{2} /\sqrt[]{3} AB/sen45° = 6/sen120° > AB /\sqrt[]{2}/2 = 6/\sqrt[]{3}/2 > AB = 6\sqrt[]{2} /\sqrt[]{3}](/latexrender/pictures/0fc6ad41439b9c4b84b918544cb076ba.png) , que racionalizando temos:
, que racionalizando temos:![AB = 2\sqrt[]{6} AB = 2\sqrt[]{6}](/latexrender/pictures/e51ecabc862672843a7dd692d6de20a2.png) .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
