Raios do círculo:
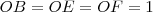
Aplicação direta do teorema de Pitágoras:

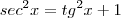
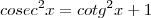
Obtemos a tangente a partir da semelhança entre os triângulos OAF e OBC, pelo caso ângulo-ângulo:
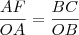

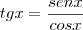
A secante, também por semelhança entre os mesmos triângulos:
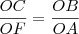
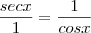
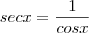
Já a cotangente, por semelhança entre os triângulos OED e OAF, também pelo caso AA pois o ângulo
 :
: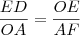

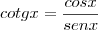
E a cosecante, também por semelhança entre os triângulos OED e OAF, segue diretamente desta relação:
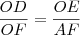

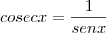



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)