Materiais sobre Cálculo.
Utilize a seção de pedidos para outros que não estejam disponíveis.
As fontes dos arquivos serão diversas e deverão ser citadas sempre que possível, mantendo totalmente os créditos dos respectivos autores.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por robertinha » Qui Mai 17, 2012 12:00
por robertinha » Qui Mai 17, 2012 12:00
clara posui em uma sala de estar um aquario em formato de paralelepipedo retangulo de altura 30 cm, largura 40 cm, e comprimento 50 cm.O volume de agua no aguario de clara é de 80% da capacidade total, o que corresponde a quantos litros? nao sei nem como começar essa conta.
-
robertinha
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mai 17, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: adm
- Andamento: cursando
 por Edu-sjc » Qui Mai 17, 2012 14:47
por Edu-sjc » Qui Mai 17, 2012 14:47
Bom a capacideda máxima de água é fácil de ser calculada:
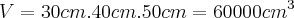
Mas o volume de água corresponde à 80% da capacidade total, logo com uma regra de três:
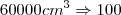
%
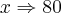
%
Logo:
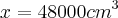
Agora é só passar para litros, nós sabemos que
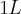
equivale a
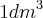
, e sabemos que:
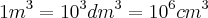
Logo:
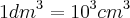
. Assim:
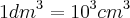
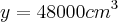
Logo há 48L de água dentro do aquário!
Deve ser isso, espero ter ajudado!flw
-
Edu-sjc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Out 26, 2011 12:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Capacidade e Proporção
por monteyrogab » Qui Abr 30, 2015 17:33
- 0 Respostas
- 1462 Exibições
- Última mensagem por monteyrogab

Qui Abr 30, 2015 17:33
Aritmética
-
- Porcentagem e medidas de capacidade
por Edmilson » Sáb Mar 08, 2014 23:23
- 1 Respostas
- 4418 Exibições
- Última mensagem por fff

Dom Mar 09, 2014 16:27
Conversão de Unidades
-
- [Volume] Volume de caixa para carrinho de mão
 por MateusDantas1 » Seg Nov 05, 2012 20:12
por MateusDantas1 » Seg Nov 05, 2012 20:12
- 0 Respostas
- 2734 Exibições
- Última mensagem por MateusDantas1

Seg Nov 05, 2012 20:12
Geometria Espacial
-
- [Cálculo do Volume] Variação do volume em porcentagem
por Douglaasag » Sex Out 10, 2014 09:23
- 0 Respostas
- 4484 Exibições
- Última mensagem por Douglaasag

Sex Out 10, 2014 09:23
Cálculo: Limites, Derivadas e Integrais
-
- volume da planta de uma piscina [volume]
 por moraesfran » Ter Nov 15, 2011 21:38
por moraesfran » Ter Nov 15, 2011 21:38
- 0 Respostas
- 2101 Exibições
- Última mensagem por moraesfran

Ter Nov 15, 2011 21:38
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



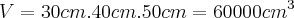
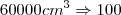 %
%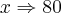 %
%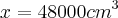
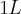 equivale a
equivale a 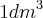 , e sabemos que:
, e sabemos que: 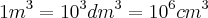
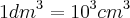 . Assim:
. Assim: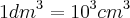
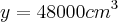


 .
.
 :
: