Limite de várias variáveis
Estou tendo um problema no seguinte limite, x e y tendem a 0, sei que o limite vai dar zero, mas não consigo resolver... se alguém conseguir me ajudar, ficaria grato
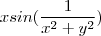
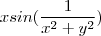
AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!
http://www.ajudamatematica.com/
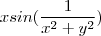
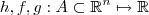 . Defina
. Defina 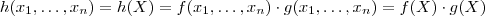 . Suponha
. Suponha  limitada , isto é , existe algum
limitada , isto é , existe algum  tal que
tal que 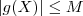 para qualquer que seja o vetor
para qualquer que seja o vetor  em
em  .
. 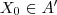 , temos
, temos 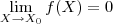 então
então 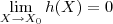 .
. representa o conjunto dos ponto de acumulação de A)
representa o conjunto dos ponto de acumulação de A) 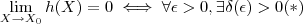 tal que se
tal que se 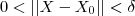 então
então  .
.  .
. 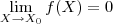 , o que significa que dado
, o que significa que dado  existe um
existe um  (correspondente) tal que
(correspondente) tal que 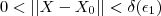 implica
implica  .
. 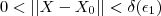 implica
implica 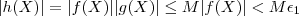 .
.  , dado
, dado 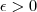 podemos tomar
podemos tomar 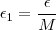 e com isso temos
e com isso temos 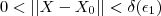 implica
implica  .
. 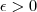 , tomando
, tomando  conseguimos um
conseguimos um 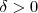 tal que se (o lardo esquerdo da implicação é verdeiro o lado direito também o é )
tal que se (o lardo esquerdo da implicação é verdeiro o lado direito também o é ) 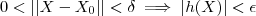 .
. 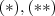 .
.  .
.  (onde :
(onde : 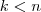 )
)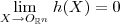 ( onde
( onde 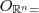 vetor nulo do R^n ) , pois
vetor nulo do R^n ) , pois 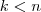 , então
, então 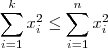 e assim
e assim  . Seja
. Seja  e
e  .
. 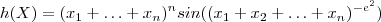 . Temos
. Temos  (Pq ??)
(Pq ??)