Eu tive duvidas quanto ao local que eu deveria postar esse "Tutorial" mas acho que aqui é apropriado.
Equações de 1º grau.
-Equações são afirmaçoes matemáticas que dizem que alguma expressão matemática é igual a outra expressão
Exemplos:

As equaçoes de primeiro grau são aquelas que contem uma só incógnita. Mas antes de tudo... O que é uma incógnita ?
Uma incógnita é um numero que desconhecemos, mas sabemos algo sobre ele. por exemplo. ALGUM NUMERO menos 10 é igual a 20...
esse numero é o que em equações chamamos de incógnitas, e tudo o que faremos é tentar descobrir que numero é esse!
Para facilitar as coisas, costumamos chamar o "ALGUM NUMERO" de uma letra, por exemplo x, ou t, ou a... em fim
Entao basicamente o que queremos fazer é descobrir esses 'numeros escondidos' mas que estão presentes numa igualdade.
Vejamos essa igualdade pra começar :
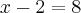
Quando olhamos essa igualdade, devemos pensar antes de tudo. Qual numero que quando voce tira 2 nós obtemos 8 ?
é nisso que se baseia o estudo das equações.
Nesse exemplo acima, algumas pessoas já percebem que x é na verdade o numero 10. Pessoas muito acostumadas com as operaçoes matemáticas... mas vejamos alguns métodos pra determinação do numero x.
Digamos que voce pode fazer QUALQUER coisa numa equação, contanto que voce faça dos dois lados a mesma coisa, mantendo a igualdade! Como numa balança em equilibrio! precisamos colocar o mesmo tanto de peso de cada lado para que a mesma continue em equilibrio.
Entao, observe :
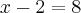
nós podemos fazer o que quisermos aqui. mas temos que manter em mente que queremos deixar o numero x sosinho do lado esquerdo da igualdade! entao vejamos. olhando só para o lado esquerdo, o que precisariamos fazer para obter apenas x e não x - 2 ?
simples, só precisamos somar 2! afinal x - 2 + 2 é x.
Fazendo isso de ambos os lados obteremos
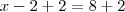

Se esse metodo ficou muito dificil pra voce, vamos tentar a mesma coisa só que de um jeito completamente diferente!
digamos que, eu posso "passar o -2 para o outro lado da equação, se eu inverter a sua operação"
Vou explicar melhor.
Qual a operação "inversa" da soma? a subtração!
entao eu posso "passar" o 2 que está subtraindo, para o outro lado, porém somando!
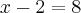
passando o -2 como +2 temos :


Bom. dai temos 2 metodos pra desvendar o "numero x" sempre que estiver somando alguma coisa ou subtraindo!
Exercicios. Tente fazer essas equações:
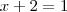
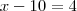
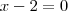
Legal, agora vamos usar as multiplicações e divisões!
vejamos outro tipo de equação:

essa é outra equação! Qual numero que quando eu multiplico por 3 resulta no numero 9 ?
Novamente, pessoas que estao acostumadas a fazer muita conta diriam rapidamente que x = 3, afinal
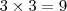
Mas vamos com calma. Vamos executar aquelas duas tecnicas para obter de verdade o nosso numero X.
a primeira tecnica era a de fazer a mesma coisa dos dois lados da equação! Vamos entao! O que nós podemos fazer para deixar o x sosinho do lado esquerdo ?
Se nós lembrarmos que qualquer numero multiplicado por um dá ele mesmo, já temos uma dica! precisamos "transformar" esse 3 em um numero 1
É só lembrarmos também que qualquer numero dividido por ele mesmo resulta em UM!
Vamos dividir por 3 ?
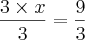

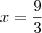

Ficou facil ? se nao ficou, vamos tentar aquele outro método. que na verdade é a mesma coisa só que visto de um outro jeito.
Qual a operação "inversa" à multiplicação ?
é a divisão!
Simples então! ao ver uma coisa como essa :

simplesmente "passe o 3 para o outro lado" dividindo!
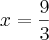
Exercicios, tente fazer o mesmo com esses :
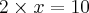
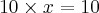
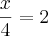
Agora por ultimo. vamos misturar todas as operações matemáticas!!! é assim que as coisas acontecem!
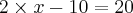
Bom, sempre que toparmos com coisas do tipo, iremos primeiro atacar as somas ou subtrações!
Passando o -10 para o outro lado como +10 ficará
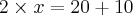

e vamos agora passar o 2 para o outro lado dividindo!
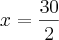

Bom, ai está. Realmente espero ter ajudado. Se tiver ruim podem jogar fora =P
Grande abraço e bons estudos.




 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
