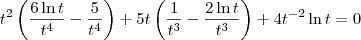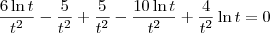MAT0130
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por borges » Sex Ago 26, 2011 22:37
por borges » Sex Ago 26, 2011 22:37
Verifique se a(s) função(s) dadas constituem solução da equação diferencial.
a) y’’ + 2y’ – 3y = 0;

(t) =
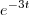
e

(t) =
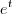
b) y’’’’ + 4y’’’ + 3y = t;

(t) = t/3 e

(t) =
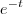
+ t/3
c)
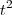
y’’ + 5t y’ + 4y = 0; t > 0;

(t) =
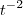
e

(t) =
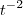
ln t
-
borges
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Abr 22, 2011 21:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por LuizAquino » Sex Ago 26, 2011 23:33
por LuizAquino » Sex Ago 26, 2011 23:33
Quais foram as suas dúvidas?
Quais foram as suas tentativas?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Neperiano » Sáb Ago 27, 2011 12:37
por Neperiano » Sáb Ago 27, 2011 12:37
Ola
É só tu derivar as duas equações que estão ao lado da função, e depois substituir e verificar se igual ao que está pedindo
Nos mostre suas tentativas
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por borges » Seg Ago 29, 2011 10:56
por borges » Seg Ago 29, 2011 10:56
Consegui fazer as letras a e b, mas a letra c, infelizmente não consegui tudo. Veja a resolução da letra c, até onde consegui. Se possível me ajude a continuar.
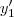
(t)=
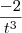
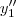
(t)=
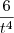
Substituindo
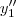
(t),
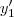
(t) e

(t) na equação temos :
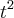
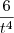
+5t
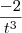
+

=0
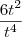
-
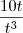
+

=0
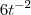
-
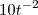
+

=0
0=0
Logo

é solução da equação.
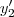
(t)=

-
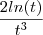
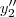
(t)=
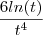
-
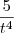
Substituindo
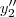
(t),
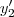
(t) e

(t) na equação temos :
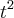
(
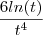
-
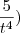
+ 5t (

-
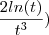
+

=0
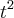
(
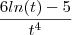
+
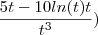
+

ln(t)=0
A partir daqui não consegui mais. Poderia me ajudar a continuar?
-
borges
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Abr 22, 2011 21:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por LuizAquino » Seg Ago 29, 2011 13:32
por LuizAquino » Seg Ago 29, 2011 13:32
borges escreveu: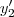
(t)=

-
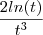
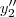
(t)=
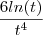
-
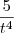
Ok.
borges escreveu: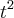
(
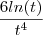
-
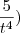
+ 5t (

-
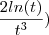
+

=0
Apenas faltou o
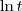
no último termo.
borges escreveu: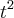
(
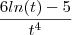
+
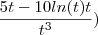
+

ln(t)=0
Faltaram dois parênteses. Um "fechando" a primeira fração e o outro "abrindo" a segunda fração.
borges escreveu:A partir daqui não consegui mais. Poderia me ajudar a continuar?
Considere a equação:
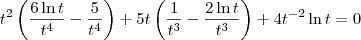
Note que ela pode ser reescrita como:
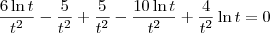
Continue a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por borges » Seg Ago 29, 2011 22:44
por borges » Seg Ago 29, 2011 22:44
ok. Obrigado.
-
borges
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Abr 22, 2011 21:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
Voltar para Equações Diferenciais Ordinárias e Aplicações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (t) =
(t) = 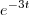 e
e  (t) =
(t) = 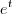
 (t) = t/3 e
(t) = t/3 e  (t) =
(t) = 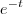 + t/3
+ t/3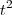 y’’ + 5t y’ + 4y = 0; t > 0;
y’’ + 5t y’ + 4y = 0; t > 0;  (t) =
(t) = 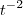 e
e  (t) =
(t) = 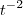 ln t
ln t
 (t) =
(t) = 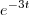 e
e  (t) =
(t) = 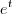
 (t) = t/3 e
(t) = t/3 e  (t) =
(t) = 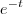 + t/3
+ t/3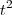 y’’ + 5t y’ + 4y = 0; t > 0;
y’’ + 5t y’ + 4y = 0; t > 0;  (t) =
(t) = 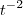 e
e  (t) =
(t) = 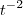 ln t
ln t


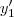 (t)=
(t)=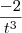
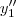 (t)=
(t)=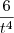
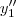 (t),
(t),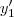 (t) e
(t) e  (t) na equação temos :
(t) na equação temos :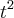
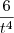 +5t
+5t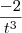 +
+  =0
=0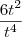 -
-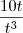 +
+ =0
=0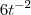 -
-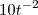 +
+ =0
=0 é solução da equação.
é solução da equação.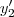 (t)=
(t)= -
-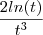
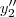 (t)=
(t)=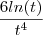 -
-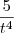
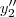 (t),
(t),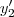 (t) e
(t) e  (t) na equação temos :
(t) na equação temos :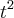 (
(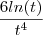 -
-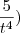 + 5t (
+ 5t ( -
-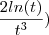 +
+  =0
=0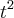 (
(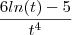 +
+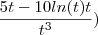 +
+  ln(t)=0
ln(t)=0
(t)=
-
(t)=
-
(
-
+ 5t (
-
+
=0
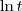 no último termo.
no último termo.(
+
+
ln(t)=0