MAT0130
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por borges » Sex Ago 26, 2011 22:37
por borges » Sex Ago 26, 2011 22:37
Verifique se a(s) função(s) dadas constituem solução da equação diferencial.
a) y’’ + 2y’ – 3y = 0;

(t) =
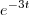
e

(t) =
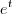
b) y’’’’ + 4y’’’ + 3y = t;

(t) = t/3 e

(t) =
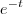
+ t/3
c)
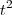
y’’ + 5t y’ + 4y = 0; t > 0;

(t) =
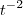
e

(t) =
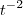
ln t
-
borges
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Abr 22, 2011 21:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por LuizAquino » Sex Ago 26, 2011 23:33
por LuizAquino » Sex Ago 26, 2011 23:33
Quais foram as suas dúvidas?
Quais foram as suas tentativas?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Neperiano » Sáb Ago 27, 2011 12:37
por Neperiano » Sáb Ago 27, 2011 12:37
Ola
É só tu derivar as duas equações que estão ao lado da função, e depois substituir e verificar se igual ao que está pedindo
Nos mostre suas tentativas
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por borges » Seg Ago 29, 2011 10:56
por borges » Seg Ago 29, 2011 10:56
Consegui fazer as letras a e b, mas a letra c, infelizmente não consegui tudo. Veja a resolução da letra c, até onde consegui. Se possível me ajude a continuar.
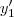
(t)=
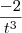
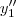
(t)=
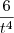
Substituindo
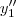
(t),
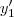
(t) e

(t) na equação temos :
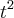
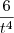
+5t
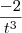
+

=0
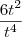
-
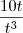
+

=0
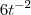
-
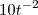
+

=0
0=0
Logo

é solução da equação.
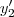
(t)=

-
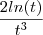
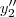
(t)=
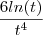
-
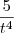
Substituindo
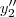
(t),
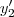
(t) e

(t) na equação temos :
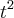
(
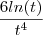
-
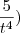
+ 5t (

-
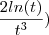
+

=0
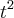
(
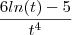
+
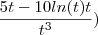
+

ln(t)=0
A partir daqui não consegui mais. Poderia me ajudar a continuar?
-
borges
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Abr 22, 2011 21:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por LuizAquino » Seg Ago 29, 2011 13:32
por LuizAquino » Seg Ago 29, 2011 13:32
borges escreveu: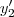
(t)=

-
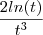
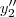
(t)=
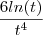
-
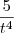
Ok.
borges escreveu: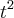
(
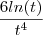
-
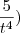
+ 5t (

-
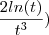
+

=0
Apenas faltou o
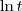
no último termo.
borges escreveu: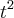
(
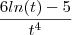
+
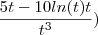
+

ln(t)=0
Faltaram dois parênteses. Um "fechando" a primeira fração e o outro "abrindo" a segunda fração.
borges escreveu:A partir daqui não consegui mais. Poderia me ajudar a continuar?
Considere a equação:
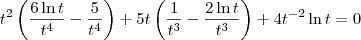
Note que ela pode ser reescrita como:
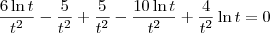
Continue a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por borges » Seg Ago 29, 2011 22:44
por borges » Seg Ago 29, 2011 22:44
ok. Obrigado.
-
borges
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Abr 22, 2011 21:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
Voltar para Equações Diferenciais Ordinárias e Aplicações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (t) =
(t) = 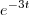 e
e  (t) =
(t) = 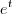
 (t) = t/3 e
(t) = t/3 e  (t) =
(t) = 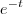 + t/3
+ t/3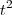 y’’ + 5t y’ + 4y = 0; t > 0;
y’’ + 5t y’ + 4y = 0; t > 0;  (t) =
(t) = 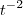 e
e  (t) =
(t) = 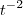 ln t
ln t
 (t) =
(t) = 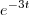 e
e  (t) =
(t) = 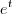
 (t) = t/3 e
(t) = t/3 e  (t) =
(t) = 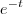 + t/3
+ t/3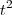 y’’ + 5t y’ + 4y = 0; t > 0;
y’’ + 5t y’ + 4y = 0; t > 0;  (t) =
(t) = 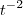 e
e  (t) =
(t) = 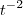 ln t
ln t


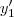 (t)=
(t)=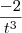
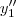 (t)=
(t)=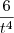
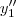 (t),
(t),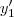 (t) e
(t) e  (t) na equação temos :
(t) na equação temos :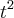
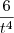 +5t
+5t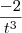 +
+  =0
=0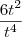 -
-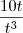 +
+ =0
=0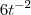 -
-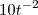 +
+ =0
=0 é solução da equação.
é solução da equação.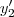 (t)=
(t)= -
-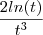
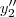 (t)=
(t)=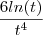 -
-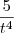
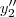 (t),
(t),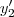 (t) e
(t) e  (t) na equação temos :
(t) na equação temos :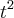 (
(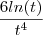 -
-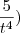 + 5t (
+ 5t ( -
-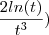 +
+  =0
=0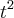 (
(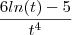 +
+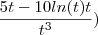 +
+  ln(t)=0
ln(t)=0
(t)=
-
(t)=
-
(
-
+ 5t (
-
+
=0
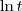 no último termo.
no último termo.(
+
+
ln(t)=0
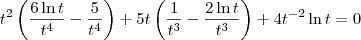
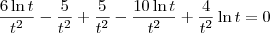



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.