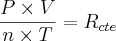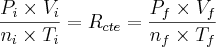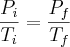[Termodinâmica] como resolver este problema?

[hugo82]

Estou com dificuldades neste problema, alguém me ajuda?
O exercicio é o seguinte:
A pressão manométrica do pneu de um automóvel é de 200 kPa antes de uma viagem, sendo de 220 kPa após um determinado percurso a um local onde a pressão atmosférica é de 90 kPa.
Considerando que o volume do pneu se mantém constante e igual a 0,035 m^3, determine o aumento percentual da temperatura absoluta do ar no pneu. Admita que Rar=0,287 kJ/(kg.K).
Refira as aproximações que efectuar.

Espero que alguém me possa ajudar, pois tenho exame hoje!
Obrigado a quem me ajudar.

[MarceloFantini]

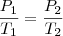Acredito que a resolução seja assim. A pressão atmosférica é 100 kPa, logo a pressão interna do pneu antes da viagem é 300 kPa. A pressão interna após a chegada no local é 310 kPa. Como o volume é constante e não há informações de que moléculas de ar sairam do pneu, podemos admitir que , e daí 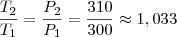, logo o aumento percentual foi de 3,3%.

[Neperiano]

Ola

Você vai tenque usar

v = R . P/T

Onde
v = volume especifíco
R = constante dos gases ideias
P = pressão
T = temperatura

Outra coisa, passe todas as informações para o SI

Para facilitar monte um desenho com as informações antes e depois e aplique na formula

Mostre sua tentativa para vermos como podemos ajudar

Atenciosamente

[MarceloFantini]

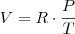As unidades parecem não bater. Se você fizer você terá que .

[Neperiano]

Ola

Porque você na passou pro SI corretamente

Transforme KJ em 1000 kg.((m^2)/s^2)

E atm para 10^5 Nm

Se não me engano é isso, tem uma tabela de conversões na intenet

Mas da sim certo

Atenciosamente

[TheoFerraz]

só o q eu sei é que:

para todo estado dum gás ideal temos:



se isso vale pra todo estado do gás, e resulta numa cte, vamos igualar!



sendo "i" inicial e "f" o estado final.

como o n (que é a quantidade de matéria) e o volume, não mudam, fica



assim como dito inicialmente

entao que dá pra ser daquele jeito dá. eu na verdade nao sabia sobre apresentada na segunda resposta.

att, theo.

[Neperiano]

Ola

hugo82, se você tiver gabarito se puder conferir se a 1 resposta está correta

Na verdade o que você escreveu é a mesma coisa que eu, você só isolou o R, e na verdade eu não coloquei o n, que para mim foi dito como m, porque o R aqui neste caso ja ta cortado com o n.

Rar=0,287 kJ/(kg.K).

Cade o Kmol? Ja foi cortado, tem duas maneiras de pegar o R, ele como valor 8,... não lembro mais, que é constante, ou pegar ele para cada tipo de material.

Atenciosamente

[hugo82]

Infelizmente não tenho a solução do problema, para ajudar.
Obrigado pela colaboração.