Obs.: Os exercicios abaixo sao retirados do livro Algebra com Aplicaçoes - Steven J. Leon.
1) Para a matriz A a seguir, use o processo de Gram-Schmidt para encontrar ortonormal para I(A).
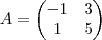
Bem primeiro, entao encontrei a base para I(A). ( I(A) é, segundo meu professor, imagem de A )
I(A) = Vetores linha não nulos da matriz A transposta apos o escalonamento.
Escalonando A transposta fica-se com a matriz:
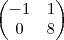
Ou seja I(A) = [(-1 , 1) , (0 , 8)] Obs.: vetores sao transpostos.
Ok tendo as base de I(A), basta aplicar Gram-Schmidt.
Onde v1 e v2 sao respectivamente (-1,1) e (0,8)
Conserva-se um vetor (normalizando-o) e acha-se o outro, ou seja:
![{u}_{1} = (-1 , 1)
\frac{1}{\sqrt[2]{2}} {u}_{1} = (-1 , 1)
\frac{1}{\sqrt[2]{2}}](/latexrender/pictures/e4ae39fd02e9ba294a180a296488ff77.png)
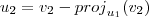
Calculando ...
![(0,8) - [(0,8).(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})].(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}}) (0,8) - [(0,8).(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})].(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})](/latexrender/pictures/6566b2ed7e243ff3dadb91a0c1b315fc.png)
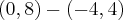
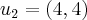 ... normalizando u2 ficamos com :
... normalizando u2 ficamos com :![{u}_{2} = (4,4). \frac{1}{4\sqrt[2]{2}} {u}_{2} = (4,4). \frac{1}{4\sqrt[2]{2}}](/latexrender/pictures/04901a4b09a0d7585cf364bdbc08f4fa.png)
![{u}_{2} = (\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}}) {u}_{2} = (\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})](/latexrender/pictures/7daa8ffddbaf21c64c146e8a2e69a9b8.png)
Bem entao os vetores ortonormais para base de I(A) sao:
![\left[ {(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} , {(\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} \right] \left[ {(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} , {(\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} \right]](/latexrender/pictures/35fe3b29950e3626115ee0de9a9d719f.png)
Esta foi minha resposta e a certa no gabarito é :
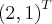
2) Fatore a matriz A ( é a mesma do exercicio de cima) em que o produto QR, onde Q é uma matriz ortogonal e R é trianular superior.
Bem esta questao, na verdade nao tenho certeza do que é pra fazer, portanto se alguem tiver algo sobre o assunto ou puder indicar um site ou video, uma vez que nao achei em nenhum livro ate agora.
3) Dada a base {(1,2,-2) , (4,3,2), (1,2,1)} para R^3 use o processo de Gram-Schmidt para encontrar uma base ortonormal. Obs.: os vetores sao transpostos.
Fiz como a primeira questao:
![{u}_{1} = (1,2,-2) . \frac{1}{\sqrt[2]{5}} {u}_{1} = (1,2,-2) . \frac{1}{\sqrt[2]{5}}](/latexrender/pictures/5c4b425be54860390a722404c69d7d49.png) (primeiro vetor normalizado)
(primeiro vetor normalizado)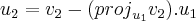
![{u}_{3} = {v}_{3} - [ ({proj}_{{u}_{1}}{v}_{3}) . {u}_{1} ] - [ ({proj}_{{u}_{2}}{v}_{3}) . {u}_{2} ] {u}_{3} = {v}_{3} - [ ({proj}_{{u}_{1}}{v}_{3}) . {u}_{1} ] - [ ({proj}_{{u}_{2}}{v}_{3}) . {u}_{2} ]](/latexrender/pictures/5bab950ab08061df492e11c10df9b096.png)
Onde, v1, v2 e v3 sao respectivamente (1,2,-2) , (4,3,2) , (1,2,1).
![{u}_{2} = (4,3,2) - 6.\left(\frac{1}{\sqrt[2]{5}},\frac{2}{\sqrt[2]{5}}, \frac{-2}{\sqrt[2]{5}}\right) {u}_{2} = (4,3,2) - 6.\left(\frac{1}{\sqrt[2]{5}},\frac{2}{\sqrt[2]{5}}, \frac{-2}{\sqrt[2]{5}}\right)](/latexrender/pictures/d6b97f163714f39c344f9d987ff84f53.png)
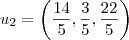 ... normalizando
... normalizando![{u}_{2} = \left(\frac{14}{\sqrt[2]{689}},\frac{3}{\sqrt[2]{689}},\frac{22}{\sqrt[2]{689}} \right) {u}_{2} = \left(\frac{14}{\sqrt[2]{689}},\frac{3}{\sqrt[2]{689}},\frac{22}{\sqrt[2]{689}} \right)](/latexrender/pictures/26d75d3534f510e5fbe0aaf9a6a4b7ec.png)
Agora u3 pra resumir ja ue sao bastantes calculos vou botar somente o que deu, mas foi feito como esta ali.
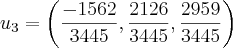 ... ja normalizado.
... ja normalizado.Bem deu isso e o gabarito diz
![\left[{{\left(1-2\alpha, \alpha \right)}^{T}| \alpha real} \right] \left[{{\left(1-2\alpha, \alpha \right)}^{T}| \alpha real} \right]](/latexrender/pictures/ac4ece6028d7f5a811df24b7c7154175.png)
Obrigado a quem ler.


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)