MAT0134
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por ewald » Sex Mai 11, 2012 15:58
por ewald » Sex Mai 11, 2012 15:58
Ola, estou tentando fazer estas questoes (abaixo) do capitulo de AL sobre vetores ortonormais. Bem acontece que a primeira o gabarito nao bate e a terceira quando vou verificar se os vetores sao realmente ortogonais entre si acontece de eles nao serem. Bem vou botar as questoes aqui embaixo e o que eu tentei fazer e se alguem tiver uma dica, correçao, ... :
Obs.: Os exercicios abaixo sao retirados do livro Algebra com Aplicaçoes - Steven J. Leon.
1) Para a matriz A a seguir, use o processo de Gram-Schmidt para encontrar ortonormal para I(A).
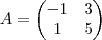
Bem primeiro, entao encontrei a base para I(A). ( I(A) é, segundo meu professor, imagem de A )
I(A) = Vetores linha não nulos da matriz A transposta apos o escalonamento.
Escalonando A transposta fica-se com a matriz:
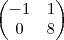
Ou seja I(A) = [(-1 , 1) , (0 , 8)] Obs.: vetores sao transpostos.
Ok tendo as base de I(A), basta aplicar Gram-Schmidt.
Onde v1 e v2 sao respectivamente (-1,1) e (0,8)
Conserva-se um vetor (normalizando-o) e acha-se o outro, ou seja:
![{u}_{1} = (-1 , 1)
\frac{1}{\sqrt[2]{2}} {u}_{1} = (-1 , 1)
\frac{1}{\sqrt[2]{2}}](/latexrender/pictures/e4ae39fd02e9ba294a180a296488ff77.png)
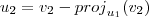
Calculando ...
![(0,8) - [(0,8).(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})].(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}}) (0,8) - [(0,8).(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})].(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})](/latexrender/pictures/6566b2ed7e243ff3dadb91a0c1b315fc.png)
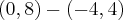
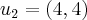
... normalizando u2 ficamos com :
![{u}_{2} = (4,4). \frac{1}{4\sqrt[2]{2}} {u}_{2} = (4,4). \frac{1}{4\sqrt[2]{2}}](/latexrender/pictures/04901a4b09a0d7585cf364bdbc08f4fa.png)
![{u}_{2} = (\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}}) {u}_{2} = (\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})](/latexrender/pictures/7daa8ffddbaf21c64c146e8a2e69a9b8.png)
Bem entao os vetores ortonormais para base de I(A) sao:
![\left[ {(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} , {(\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} \right] \left[ {(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} , {(\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} \right]](/latexrender/pictures/35fe3b29950e3626115ee0de9a9d719f.png)
Esta foi minha resposta e a certa no gabarito é :
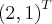
2) Fatore a matriz A ( é a mesma do exercicio de cima) em que o produto QR, onde Q é uma matriz ortogonal e R é trianular superior.
Bem esta questao, na verdade nao tenho certeza do que é pra fazer, portanto se alguem tiver algo sobre o assunto ou puder indicar um site ou video, uma vez que nao achei em nenhum livro ate agora.
3) Dada a base {(1,2,-2) , (4,3,2), (1,2,1)} para R^3 use o processo de Gram-Schmidt para encontrar uma base ortonormal. Obs.: os vetores sao transpostos.
Fiz como a primeira questao:
![{u}_{1} = (1,2,-2) . \frac{1}{\sqrt[2]{5}} {u}_{1} = (1,2,-2) . \frac{1}{\sqrt[2]{5}}](/latexrender/pictures/5c4b425be54860390a722404c69d7d49.png)
(primeiro vetor normalizado)
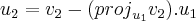
![{u}_{3} = {v}_{3} - [ ({proj}_{{u}_{1}}{v}_{3}) . {u}_{1} ] - [ ({proj}_{{u}_{2}}{v}_{3}) . {u}_{2} ] {u}_{3} = {v}_{3} - [ ({proj}_{{u}_{1}}{v}_{3}) . {u}_{1} ] - [ ({proj}_{{u}_{2}}{v}_{3}) . {u}_{2} ]](/latexrender/pictures/5bab950ab08061df492e11c10df9b096.png)
Onde, v1, v2 e v3 sao respectivamente (1,2,-2) , (4,3,2) , (1,2,1).
![{u}_{2} = (4,3,2) - 6.\left(\frac{1}{\sqrt[2]{5}},\frac{2}{\sqrt[2]{5}}, \frac{-2}{\sqrt[2]{5}}\right) {u}_{2} = (4,3,2) - 6.\left(\frac{1}{\sqrt[2]{5}},\frac{2}{\sqrt[2]{5}}, \frac{-2}{\sqrt[2]{5}}\right)](/latexrender/pictures/d6b97f163714f39c344f9d987ff84f53.png)
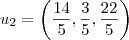
... normalizando
![{u}_{2} = \left(\frac{14}{\sqrt[2]{689}},\frac{3}{\sqrt[2]{689}},\frac{22}{\sqrt[2]{689}} \right) {u}_{2} = \left(\frac{14}{\sqrt[2]{689}},\frac{3}{\sqrt[2]{689}},\frac{22}{\sqrt[2]{689}} \right)](/latexrender/pictures/26d75d3534f510e5fbe0aaf9a6a4b7ec.png)
Agora u3 pra resumir ja ue sao bastantes calculos vou botar somente o que deu, mas foi feito como esta ali.
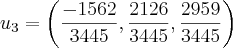
... ja normalizado.
Bem deu isso e o gabarito diz
![\left[{{\left(1-2\alpha, \alpha \right)}^{T}| \alpha real} \right] \left[{{\left(1-2\alpha, \alpha \right)}^{T}| \alpha real} \right]](/latexrender/pictures/ac4ece6028d7f5a811df24b7c7154175.png)
Obrigado a quem ler.
-
ewald
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Qui Mai 05, 2011 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
 por ewald » Sex Mai 11, 2012 22:21
por ewald » Sex Mai 11, 2012 22:21
Ok, esquece a questao 3,, embora nao esteja batendo com o gabarito, o qual parece estar errado, consegui deixa-los ortonormais. Meu erro foi na verdade ridiculo. Errei na normalizaçao do 1º vetor e o erro obviamente se propagou.
No entanto as outras continuo sem saber, alias a 1ª eu realmente acho que o gabarito esta trocado.
Obrigado
-
ewald
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Qui Mai 05, 2011 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
Voltar para Introdução à Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
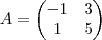
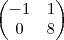
![{u}_{1} = (-1 , 1)
\frac{1}{\sqrt[2]{2}} {u}_{1} = (-1 , 1)
\frac{1}{\sqrt[2]{2}}](/latexrender/pictures/e4ae39fd02e9ba294a180a296488ff77.png)
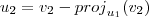
![(0,8) - [(0,8).(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})].(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}}) (0,8) - [(0,8).(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})].(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})](/latexrender/pictures/6566b2ed7e243ff3dadb91a0c1b315fc.png)
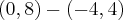
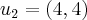 ... normalizando u2 ficamos com :
... normalizando u2 ficamos com :![{u}_{2} = (4,4). \frac{1}{4\sqrt[2]{2}} {u}_{2} = (4,4). \frac{1}{4\sqrt[2]{2}}](/latexrender/pictures/04901a4b09a0d7585cf364bdbc08f4fa.png)
![{u}_{2} = (\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}}) {u}_{2} = (\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})](/latexrender/pictures/7daa8ffddbaf21c64c146e8a2e69a9b8.png)
![\left[ {(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} , {(\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} \right] \left[ {(-\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} , {(\frac{1}{\sqrt[2]{2}},\frac{1}{\sqrt[2]{2}})}^{T} \right]](/latexrender/pictures/35fe3b29950e3626115ee0de9a9d719f.png)
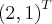
![{u}_{1} = (1,2,-2) . \frac{1}{\sqrt[2]{5}} {u}_{1} = (1,2,-2) . \frac{1}{\sqrt[2]{5}}](/latexrender/pictures/5c4b425be54860390a722404c69d7d49.png) (primeiro vetor normalizado)
(primeiro vetor normalizado)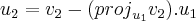
![{u}_{3} = {v}_{3} - [ ({proj}_{{u}_{1}}{v}_{3}) . {u}_{1} ] - [ ({proj}_{{u}_{2}}{v}_{3}) . {u}_{2} ] {u}_{3} = {v}_{3} - [ ({proj}_{{u}_{1}}{v}_{3}) . {u}_{1} ] - [ ({proj}_{{u}_{2}}{v}_{3}) . {u}_{2} ]](/latexrender/pictures/5bab950ab08061df492e11c10df9b096.png)
![{u}_{2} = (4,3,2) - 6.\left(\frac{1}{\sqrt[2]{5}},\frac{2}{\sqrt[2]{5}}, \frac{-2}{\sqrt[2]{5}}\right) {u}_{2} = (4,3,2) - 6.\left(\frac{1}{\sqrt[2]{5}},\frac{2}{\sqrt[2]{5}}, \frac{-2}{\sqrt[2]{5}}\right)](/latexrender/pictures/d6b97f163714f39c344f9d987ff84f53.png)
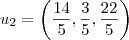 ... normalizando
... normalizando![{u}_{2} = \left(\frac{14}{\sqrt[2]{689}},\frac{3}{\sqrt[2]{689}},\frac{22}{\sqrt[2]{689}} \right) {u}_{2} = \left(\frac{14}{\sqrt[2]{689}},\frac{3}{\sqrt[2]{689}},\frac{22}{\sqrt[2]{689}} \right)](/latexrender/pictures/26d75d3534f510e5fbe0aaf9a6a4b7ec.png)
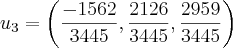 ... ja normalizado.
... ja normalizado.![\left[{{\left(1-2\alpha, \alpha \right)}^{T}| \alpha real} \right] \left[{{\left(1-2\alpha, \alpha \right)}^{T}| \alpha real} \right]](/latexrender/pictures/ac4ece6028d7f5a811df24b7c7154175.png)


 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: