MarceloFantini escreveu:Ewald, por favor use LaTeX, veja a regra número 2 do fórum. Sobre a questão, qual foi a sua resposta para o item b?
Ok, como era pouca coisa que precisava botar pelo latex eu achei que nao faria muita diferença, mas ja que insiste...
8. Considere os vetores
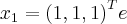
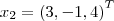
(a)
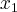
e

geram R³? Explique.
(b) Seja

um terceiro vetor em R³ e defina X = {

}. Que condição (ou condições) X tem que satisfazer para que

formem uma base para R³?
(c) Encontre um terceiro vetor

que estenda o conjunto {

} a uma base para R³.
Agora quanto minha resposta da alternativa "b":
R: X tem de ser linearmente independente e também tem de ser gerador do R³. (Sendo que no gabarito diz Linearmente independente e gerar R³)
Ta complementando um pouco, eu tentei fazer a "c" mostrando que os 3 vetores sao linearmente independentes (primeiramente) dizendo que o

é o vetor v=(
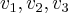
), montando entao uma matriz, escalonando ... enfim todo processo para provar que um conjunto de vetores sao L.I. e, no entanto, so consegui muitas variaveis e nenhuma resposta.
Obs.: Tentei tambem mostrar que gera o R³, mas , de novo, so consegui muitas variaveis.
Bem é isso.




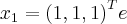
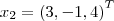
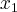 e
e  geram R³? Explique.
geram R³? Explique. um terceiro vetor em R³ e defina X = {
um terceiro vetor em R³ e defina X = { }. Que condição (ou condições) X tem que satisfazer para que
}. Que condição (ou condições) X tem que satisfazer para que  } a uma base para R³.
} a uma base para R³.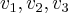 ), montando entao uma matriz, escalonando ... enfim todo processo para provar que um conjunto de vetores sao L.I. e, no entanto, so consegui muitas variaveis e nenhuma resposta.
), montando entao uma matriz, escalonando ... enfim todo processo para provar que um conjunto de vetores sao L.I. e, no entanto, so consegui muitas variaveis e nenhuma resposta.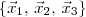 seja uma base para
seja uma base para 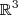 , você já sabe que esse conjunto deve ser L. I. e gerar
, você já sabe que esse conjunto deve ser L. I. e gerar 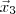 tal que aquele conjunto seja L. I. e gere
tal que aquele conjunto seja L. I. e gere 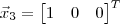 .
.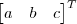
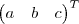

 .
.
 :
: