- Código: Selecionar todos
[tex]x^2+lnx = 0[/tex]
Eu queria saber apenas por onde começar.. obrigado

[tex]x^2+lnx = 0[/tex]
zifles2012 escreveu:De acordo com o método de Newton descubra as raizes da função
Eu queria saber apenas por onde começar.. obrigado

 ), podemos criar a função
), podemos criar a função  . O objetivo é determinar a raiz (ou raízes) dessa função. Ou seja, o valor de x tal que f(x) = 0.
. O objetivo é determinar a raiz (ou raízes) dessa função. Ou seja, o valor de x tal que f(x) = 0. . Desse modo, você terá o esquema:
. Desse modo, você terá o esquema:
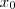 e efetue o processo iterativo quantos passos desejar. Por exemplo, você pode parar em um passo k tal que
e efetue o processo iterativo quantos passos desejar. Por exemplo, você pode parar em um passo k tal que  seja tão próximo de zero quanto você deseja.
seja tão próximo de zero quanto você deseja.
Voltar para Cálculo Numérico e Aplicações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.